Overview
Eigenvector centrality quantifies a node's influence within a graph. A node's importance is determined by its neighbors—it is both influenced by them and exerts influence on them. However, not all connections are equal; a node's centrality increases if it is connected to other highly influential nodes.
Eigenvector centrality takes on values between 0 to 1, nodes with higher centralities are more influential in the network.
Concepts
Eigenvector Centrality
The influence of a node is computed in a recursive way. Consider the graph below, and assume that nodes receive influence through incoming edges. In the adjacency matrix A, element Aij reflects the number of incoming edges of node i. Initially, each node is randomly assigned a centrality value — all set to 1 as an example —represented by the vector c(0).

In each round of influence propagation, a node's centrality is updated as the sum of centralities of all its incoming neighbors. In the first round, this operation is equivalent to multiplying the vector c(0) by the matrix A, i.e., c(1) = Ac(0). Afterward, the L2-normalization is applied to rescale the vector c(1):

After k rounds, c(k) is computed by c(k) = Ac(k-1). As k grows, c(k) stabilizes. In this example, stabilization is reached after approximately 20 rounds. The elements in c(k) represent the centrality of the corresponding nodes.

The algorithm continues until the sum of changes of all elements in c(k) converges to within some tolerance, or the maximum iteration rounds is met.
Eigenvalue and Eigenvector
Given that A is an n x n square matrix, λ is a constant, and x is a non-zero n x 1 vector. If the equation Ax = λx is true, then λ is called the eigenvalue of A, and x is the eigenvector of A that corresponds to λ.
The above adjacency matrix A has four eigenvalues λ1, λ2, λ3 and λ4 that correspond to eigenvectors x1, x2, x3 and x4, respectively. x1 is the eigenvector of the eigenvalue λ1 which has the largtest absolute value. λ1 is the dominant eigenvalue, and x1 the dominant eigenvector.
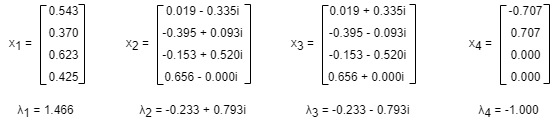
In fact, as k grows, c(k) always converges to x1, regardless of how c(0) is initialized. This phenomenon is explained by the Perron–Frobenius theorem. Therefore, computing the eigenvector centrality of nodes in a graph is equivalent to finding the dominant eigenvector of the adjacency matrix A.
Considerations
- To solve the influence leak problem in acyclic digraphs, the algorithm adopts the sum of adjacency matrix and unit matrix (i.e.,
A = A + I) rather than the adjacency matrix itself. - A self-loop counts as one in-link and one out-link.
Example Graph
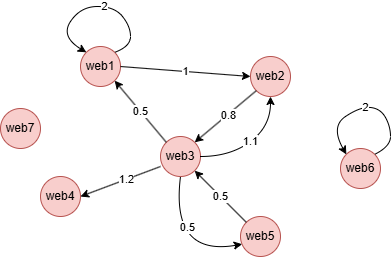
Run the following statements on an empty graph to define its structure and insert data:
ALTER GRAPH CURRENT_GRAPH ADD NODE {
web ()
};
ALTER GRAPH CURRENT_GRAPH ADD EDGE {
link ()-[{value float}]->()
};
INSERT (web1:web {_id: "web1"}),
(web2:web {_id: "web2"}),
(web3:web {_id: "web3"}),
(web4:web {_id: "web4"}),
(web5:web {_id: "web5"}),
(web6:web {_id: "web6"}),
(web7:web {_id: "web7"}),
(web1)-[:link {value: 2}]->(web1),
(web1)-[:link {value: 1}]->(web2),
(web2)-[:link {value: 0.8}]->(web3),
(web3)-[:link {value: 0.5}]->(web1),
(web3)-[:link {value: 1.1}]->(web2),
(web3)-[:link {value: 1.2}]->(web4),
(web3)-[:link {value: 0.5}]->(web5),
(web5)-[:link {value: 0.5}]->(web3),
(web6)-[:link {value: 2}]->(web6);
create().node_schema("web").edge_schema("link");
create().edge_property(@link, "value", float);
insert().into(@web).nodes([{_id:"web1"}, {_id:"web2"}, {_id:"web3"}, {_id:"web4"}, {_id:"web5"}, {_id:"web6"}, {_id:"web7"}]);
insert().into(@link).edges([{_from:"web1", _to:"web1",value:2}, {_from:"web1", _to:"web2",value:1}, {_from:"web2", _to:"web3",value:0.8}, {_from:"web3", _to:"web1",value:0.5}, {_from:"web3", _to:"web2",value:1.1}, {_from:"web3", _to:"web4",value:1.2}, {_from:"web3", _to:"web5",value:0.5}, {_from:"web5", _to:"web3",value:0.5}, {_from:"web6", _to:"web6",value:2}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: eigenvector_centrality
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
max_loop_num |
Integer | ≥1 | 20 |
Yes | The maximum number of iteration rounds. The algorithm terminates after all iterations are completed. |
tolerance |
Float | (0,1) | 0.001 |
Yes | The algorithm terminates when the changes in all scores between iterations are less than the specified tolerance, indicating that the result is stable. |
edge_weight_property |
"<@schema.?><property>" |
/ | / | Yes | A numeric edge property used as weights in the adjacency matrix A; edges without this property are ignored. |
direction |
String | in, out |
/ | Yes | Constructs the adjacency matrix A with the in-links (in) or out-links (out) of each node. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results. |
limit |
Integer | ≥-1 | -1 |
Yes | Limits the number of results returned; -1 includes all results. |
order |
String | asc, desc |
/ | Yes | Sorts the results by eigenvector_centrality. |
File Writeback
CALL algo.eigenvector_centrality.write("my_hdc_graph", {
return_id_uuid: "id",
max_loop_num: 50,
tolerance: 0.000001,
direction: "in",
order: "desc"
}, {
file: {
filename: "eigenvector_centrality"
}
})
algo(eigenvector_centrality).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
max_loop_num: 50,
tolerance: 0.000001,
direction: "in",
order: "desc"
}).write({
file: {
filename: "eigenvector_centrality"
}
})
Result:
_id,eigenvector_centrality
web1,0.573612
web2,0.573612
web3,0.460001
web5,0.255281
web4,0.255281
web6,1.35778e-05
web7,6.32265e-15
DB Writeback
Writes the eigenvector_centrality values from the results to the specified node property. The property type is double.
CALL algo.eigenvector_centrality.write("my_hdc_graph", {
edge_weight_property: "@link.value"
}, {
db: {
property: "ec"
}
})
algo(eigenvector_centrality).params({
projection: "my_hdc_graph",
edge_weight_property: "@link.value"
}).write({
db:{
property: 'ec'
}
})
Full Return
CALL algo.eigenvector_centrality.run("my_hdc_graph", {
return_id_uuid: "id",
max_loop_num: 300,
tolerance: 0.000001,
edge_weight_property: "value",
direction: "in",
order: "desc"
}) YIELD ec
RETURN ec
exec{
algo(eigenvector_centrality).params({
return_id_uuid: "id",
max_loop_num: 300,
tolerance: 0.000001,
edge_weight_property: "value",
direction: "in",
order: "desc"
}) as ec
return ec
} on my_hdc_graph
Result:
| _id | eigenvector_centrality |
|---|---|
| web1 | 0.835474799052068 |
| web2 | 0.497522870627321 |
| web3 | 0.198903901628052 |
| web4 | 0.112638313459419 |
| web5 | 0.046932628743156 |
| web6 | 0.000173115768280974 |
| web7 | 3.67918716589409e-105 |
Stream Return
CALL algo.eigenvector_centrality.stream("my_hdc_graph", {
return_id_uuid: "id",
max_loop_num: 300,
tolerance: 0.000001,
edge_weight_property: "value",
direction: "in",
order: "desc"
}) YIELD ec
RETURN ec
exec{
algo(eigenvector_centrality).params({
return_id_uuid: "id",
max_loop_num: 300,
tolerance: 0.000001,
edge_weight_property: "value",
direction: "in",
order: "desc"
}).stream() as ec
return ec
} on my_hdc_graph
Result:
| _id | eigenvector_centrality |
|---|---|
| web1 | 0.835474799052068 |
| web2 | 0.497522870627321 |
| web3 | 0.198903901628052 |
| web4 | 0.112638313459419 |
| web5 | 0.046932628743156 |
| web6 | 0.000173115768280974 |
| web7 | 3.67918716589409e-105 |

