Overview
The k-Edge Connected Components algorithm aims to find groups of nodes that have strong interconnections based on their edges. By considering the connectivity of edges rather than just the nodes themselves, the algorithm can reveal clusters or communities within the graph where nodes are tightly linked to each other. This information can be valuable for various applications, including social network analysis, web graph analysis, biological network analysis, and more.
Related material of the algorithm:
- T. Wang, Y. Zhang, F.Y.L. Chin, H. Ting, Y.H. Tsin, S. Poon, A Simple Algorithm for Finding All k-Edge-Connected Components (2015)
Concepts
Edge Connectivity
The edge connectivity of a graph is a measure that quantifies the minimum number of edges that need to be removed in order to disconnect the graph or reduce its connectivity. It represents the resilience of a graph against edge failures. Given a graph G = (V, E), G is k-edge connected if it remains connected after the removal of any k-1 or fewer edges from G.
The edge connectivity can also be interpreted as the maximum number of edge-disjoint paths between any two nodes in the graph. If the edge connectivity of a graph is k, it means that there are k edge-disjoint paths between any pair of nodes in the graph.
Below shows a 3-edge connected graph and the edge-disjoint paths between each node pair.
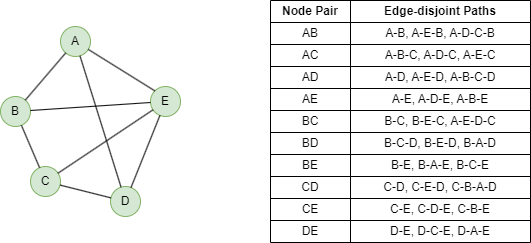
Edge-disjoint paths are paths that do not have any edge in common.
k-Edge Connected Components
Instead of determining whether the entire graph G is k-edge connected, the k-Edge Connected Components algorithm is interested in finding the maximal subsets of nodes Vi ⊆ V, where the kccs induced by Vi are k-edge connected.
For example, in social networks, finding a group of people who are strongly connected is more important than computing the connectivity of the entire social network.
Considerations
- For k = 1, this problem is equivalent to finding the connected components of G.
- The k-Edge Connected Component algorithm ignores the direction of edges but calculates them as undirected edges.
Example Graph
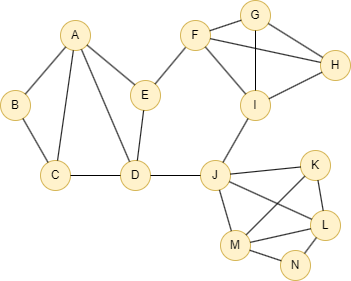
Run the following statements on an empty graph to define its structure and insert data:
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(H:default {_id: "H"}),
(I:default {_id: "I"}),
(J:default {_id: "J"}),
(K:default {_id: "K"}),
(L:default {_id: "L"}),
(M:default {_id: "M"}),
(N:default {_id: "N"}),
(A)-[:default]->(B),
(B)-[:default]->(C),
(A)-[:default]->(C),
(A)-[:default]->(D),
(A)-[:default]->(E),
(C)-[:default]->(D),
(E)-[:default]->(D),
(E)-[:default]->(F),
(D)-[:default]->(J),
(F)-[:default]->(G),
(F)-[:default]->(I),
(G)-[:default]->(H),
(F)-[:default]->(H),
(G)-[:default]->(I),
(H)-[:default]->(I),
(I)-[:default]->(J),
(J)-[:default]->(K),
(J)-[:default]->(M),
(K)-[:default]->(L),
(J)-[:default]->(L),
(M)-[:default]->(K),
(M)-[:default]->(L),
(M)-[:default]->(N),
(N)-[:default]->(L);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"}, {_id:"I"}, {_id:"J"}, {_id:"K"}, {_id:"L"}, {_id:"M"}, {_id:"N"}]);
insert().into(@default).edges([{_from:"A", _to:"B"}, {_from:"B", _to:"C"}, {_from:"A", _to:"C"}, {_from:"A", _to:"D"}, {_from:"A", _to:"E"}, {_from:"C", _to:"D"}, {_from:"E", _to:"D"}, {_from:"E", _to:"F"}, {_from:"D", _to:"J"}, {_from:"F", _to:"G"}, {_from:"F", _to:"I"}, {_from:"G", _to:"H"}, {_from:"F", _to:"H"}, {_from:"G", _to:"I"}, {_from:"H", _to:"I"}, {_from:"I", _to:"J"}, {_from:"J", _to:"K"}, {_from:"J", _to:"M"}, {_from:"K", _to:"L"}, {_from:"J", _to:"L"}, {_from:"M", _to:"K"}, {_from:"M", _to:"L"}, {_from:"M", _to:"N"}, {_from:"N", _to:"L"}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: kcc
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
k |
Integer | >1 | / | No | Specifies k to ensure k edge-disjoint paths exist between any pair of nodes in the k-edge connected components. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results. |
File Writeback
CALL algo.kcc.write("my_hdc_graph", {
k: 3,
return_id_uuid: "id"
}, {
file: {
filename: "kcc_result"
}
})
algo(kcc).params({
projection: "my_hdc_graph",
k: 3,
return_id_uuid: "id"
}).write({
file: {
filename: "kcc_result"
}
})
_ids
M,J,K,L
G,F,H,I

