Overview

The k-Truss algorithm identifies the maximal cohesive subgraph called truss in the graph. It has wide-ranging applications across various domains, including social networks, biological networks, and transportation networks. By uncovering communities or clusters of closely related nodes, the k-Truss algorithm provides valuable insights into the structure and connectivity of complex networks.

k-Truss were originally defined by J. Cohen in 2005:

• J. Cohen, Trusses: Cohesive Subgraphs for Social Network Analysis (2005)

Concepts

k-Truss

The truss is motivated by a natural observation of social cohesion: if two people are strongly tied, it is likely that they also share ties to others. k-Truss is thus created in this way: a tie between A and B is considered legitimate only if supported by at least k–2 other people who are each tied to A and to B. In other words, each edge in a k-truss joins two nodes that have at least k–2 common neighbors.

The formal definition is, a k-truss is a maximal subgraph in the graph such that each edge is supported by at least k–2 pairs of edges making triangles with the that edge.

The entire graph is shown below, the 3-truss and 4-truss are highlighted in red. This graph does not have truss with 5 or larger value of k.

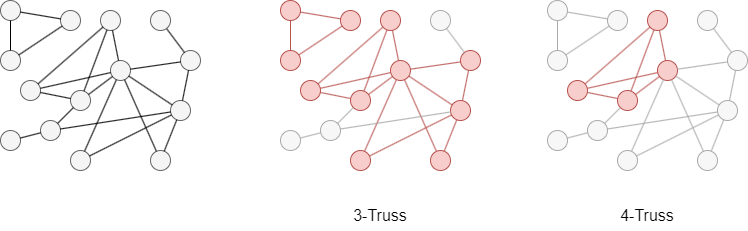
Ultipa's k-Truss algorithm identifies the maximal truss in each connected component.

Considerations

• At least 3 nodes are contained in a truss (when k≥3).
• In a complex graph where multiple edges can exist between two nodes, the triangles in a truss are counted by edges. Please also refer to the Triangle Counting algorithm.
• The k-Truss algorithm ignores the direction of edges but calculates them as undirected edges.

Example Graph

To create this graph:

// Runs each row separately in order in an empty graphset
insert().into(@default).nodes([{_id:"a"}, {_id:"b"}, {_id:"c"}, {_id:"d"}, {_id:"e"}, {_id:"f"}, {_id:"g"}, {_id:"h"}, {_id:"i"}, {_id:"j"}, {_id:"k"}, {_id:"l"}, {_id:"m"}])
insert().into(@default).edges([{_from:"b", _to:"a"}, {_from:"d", _to:"a"}, {_from:"c", _to:"a"}, {_from:"d", _to:"c"}, {_from:"f", _to:"a"}, {_from:"f", _to:"d"}, {_from:"d", _to:"f"}, {_from:"f", _to:"d"}, {_from:"d", _to:"e"}, {_from:"e", _to:"f"}, {_from:"f", _to:"c"}, {_from:"c", _to:"h"}, {_from:"i", _to:"m"}, {_from:"i", _to:"g"}, {_from:"k", _to:"c"}, {_from:"k", _to:"c"}, {_from:"k", _to:"f"}, {_from:"j", _to:"l"}, {_from:"k", _to:"l"}, {_from:"g", _to:"k"}, {_from:"m", _to:"k"}, {_from:"l", _to:"f"}, {_from:"m", _to:"f"}, {_from:"f", _to:"g"}, {_from:"g", _to:"m"}, {_from:"m", _to:"l"}])

Creating HDC Graph

To load the entire graph to the HDC server hdc-server-1 as hdc_ktruss:

CALL hdc.graph.create("hdc-server-1", "hdc_ktruss", {
  nodes: {"*": ["*"]},
  edges: {"*": ["*"]},
  direction: "undirected",
  load_id: true,
  update: "static",
  query: "query",
  default: false
})

hdc.graph.create("hdc_ktruss", {
  nodes: {"*": ["*"]},
  edges: {"*": ["*"]},
  direction: "undirected",
  load_id: true,
  update: "static",
  query: "query",
  default: false
}).to("hdc-server-1")

Parameters

Algorithm name: k_truss

File Writeback

CALL algo.k_truss.write("hdc_ktruss", {
  params: {
    k: 4,
    return_id_uuid: "id"
  },
  return_params: {
    file: {
      filename: "4truss.txt"
    }
  }
})

algo(k_truss).params({
  project: "hdc_ktruss",
  k: 4,
  return_id_uuid: "id"  
}).write({
  file: {
    filename: "4truss.txt"
  }
})

Result:

_id
e--[110]--f
k--[117]--f
k--[119]--l
m--[121]--k
m--[123]--f
m--[126]--l
c--[103]--a
g--[120]--k
g--[125]--m
d--[102]--a
d--[104]--c
d--[107]--f
d--[109]--e
f--[105]--a
f--[106]--d
f--[108]--d
f--[111]--c
f--[124]--g
l--[122]--f

Full Return

CALL algo.k_truss("hdc_ktruss", {
  params: {
    k: 5
  },
  return_params: {}
}) YIELD truss
RETURN truss

exec{
  algo(k_truss).params({
    k: 5
  }) as truss
  return truss
} on hdc_ktruss

Result:

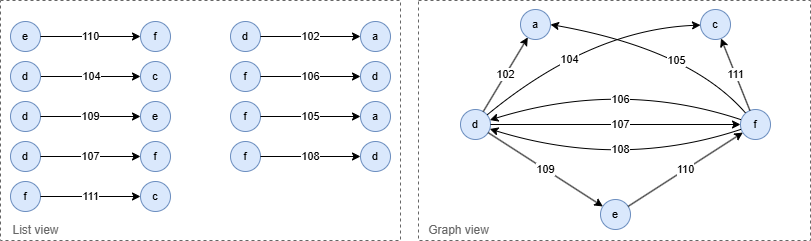
Stream Return

CALL algo.k_truss("hdc_ktruss", {
  params: {
    k: 5
  },
  return_params: {
    stream: {}
  }
}) YIELD truss5
FOR node IN pnodes(truss5)
RETURN collect_list(node._id)

exec{
  algo(k_truss).params({
    k: 5
  }).stream() as truss5
 uncollect pnodes(truss5) as node
 return collect(node._id)
} on hdc_ktruss

["d","a","d","c","d","f","d","e","f","a","f","d","f","d","f","c","e","f"]