Overview
The k-Means algorithm is a widely used clustering technique that partitions nodes in a graph into k clusters based on their similarity. Each node is assigned to the cluster whose centroid is closest, according to a specified distance metric. Common metrics include Euclidean distance and cosine similarity.
The concept of the k-Means algorithm dates back to 1957, but it was formally named and popularized by J. MacQueen in 1967:
- J. MacQueen, Some methods for classification and analysis of multivariate observations (1967)
Since then, the algorithm has been widely applied across various domains, including vector quantization, clustering analysis, feature learning, computer vision, and more. It is often used either as a preprocessing step for other algorithms or as a standalone method for exploratory data analysis.
Concepts
Centroid
The centroid, or geometric center, of an object in an N-dimensional space is the average position of all its points across each of the N coordinate directions.
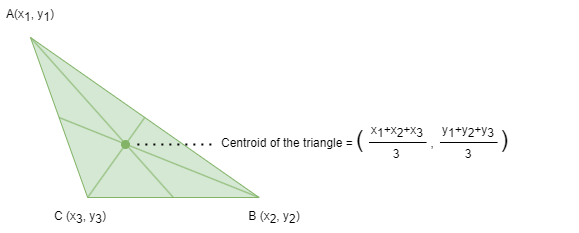
In the context of clustering algorithms such as k-Means, a centroid refers to the geometric center of a cluster. When node features are defined using multiple node properties, the centroid summarizes those features by averaging them across all nodes in the cluster. To find the centroid of a cluster, the algorithm calculates the mean feature value of each feature dimension from the nodes assigned to that cluster.
The algorithm starts by selecting k initial centroids, either manually or by random sampling.
Distance Metrics
Ultipa's k-Means algorithm computes distance between a node and a centroid through Euclidean Distance or Cosine Similarity.
Clustering Iterations
During each iterative process of k-Means, each node calculates its distance to each of the current cluster centroids and is assigned to the cluster with the closest centroid. Once all nodes have been assigned to clusters, the centroids are updated by recalculating the mean feature values of the nodes within each cluster.
The iteration ends when the clustering results stabilize to certain threshold, or the maximum number of iterations is reached.
Considerations
- The success of the k-Means algorithm depends on appropriately choosing the value of k and selecting appropriate distance metrics for the given problem. The selection of the initial centroids also affects the final clustering results.
- If two or more identical centroids exist, only one of them will take effect, while the other equivalent centroids will form empty clusters.
Example Graph
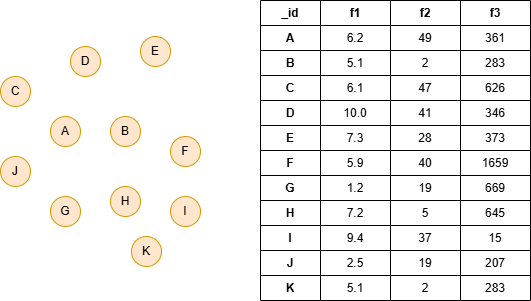
Run the following statements on an empty graph to define its structure and insert data:
ALTER NODE default ADD PROPERTY {
f1 float, f2 int32, f3 int32
};
INSERT (:default {_id:"A", f1:6.2, f2:49, f3:361}),
(:default {_id:"B", f1:5.1, f2:2, f3:283}),
(:default {_id:"C", f1:6.1, f2:47, f3:626}),
(:default {_id:"D", f1:10.0, f2:41, f3:346}),
(:default {_id:"E", f1:7.3, f2:28, f3:373}),
(:default {_id:"F", f1:5.9, f2:40, f3:1659}),
(:default {_id:"G", f1:1.2, f2:19, f3:669}),
(:default {_id:"H", f1:7.2, f2:5, f3:645}),
(:default {_id:"I", f1:9.4, f2:37, f3:15}),
(:default {_id:"J", f1:2.5, f2:19, f3:207}),
(:default {_id:"K", f1:5.1, f2:2, f3:283});
create().node_property(@default,"f1",float).node_property(@default,"f2",int32).node_property(@default,"f3",int32);
insert().into(@default).nodes([{_id:"A", f1:6.2, f2:49, f3:361}, {_id:"B", f1:5.1, f2:2, f3:283}, {_id:"C", f1:6.1, f2:47, f3:626}, {_id:"D", f1:10.0, f2:41, f3:346}, {_id:"E", f1:7.3, f2:28, f3:373}, {_id:"F", f1:5.9, f2:40, f3:1659}, {_id:"G", f1:1.2, f2:19, f3:669}, {_id:"H", f1:7.2, f2:5, f3:645}, {_id:"I", f1:9.4, f2:37, f3:15}, {_id:"J", f1:2.5, f2:19, f3:207}, {_id:"K", f1:5.1, f2:2, f3:283}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: k_means
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
start_ids |
[]_id |
/ | / | Yes | Specifies nodes as the initial centroids by their _id. The length of the array must be equal to k. The system will determine them if it is unset. |
start_uuids |
[]_uuid |
/ | / | Yes | Specifies nodes as the initial centroids by their _uuid. The length of the array must be equal to k. The system will determine them if it is unset. |
k |
Integer | [1, |V|] |
1 |
No | Specifies the number of desired clusters (|V| is the total number of nodes in the graph). |
distance_type |
Integer | 1, 2 |
1 |
Yes | Specifies the type of the distance metric. Set to 1 for Euclidean Distance, and 2 for Cosine Similarity. |
node_schema_property |
[]"<@schema.?><property>" |
/ | / | No | Numeric node properties used as features; at least two properties are required. |
loop_num |
Integer | ≥1 | / | No | The maximum number of iterations. The algorithm will terminate after completing all rounds. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results. |
File Writeback
CALL algo.k_means.write("my_hdc_graph", {
return_id_uuid: "id",
start_ids: ["A", "B", "E"],
k: 3,
distance_type: 2,
node_schema_property: ["f1", "f2", "f3"],
loop_num: 3
}, {
file: {
filename: "communities"
}
})
algo(k_means).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
start_ids: ["A", "B", "E"],
k: 3,
distance_type: 2,
node_schema_property: ["f1", "f2", "f3"],
loop_num: 3
}).write({
file: {
filename: "communities"
}
})
Result:
community id:ids
0:I
1:F,H,B,K,G
2:J,D,A,E,C
Full Return
CALL algo.k_means.run("my_hdc_graph", {
return_id_uuid: "id",
start_ids: ["A", "B", "E"],
k: 3,
distance_type: 1,
node_schema_property: ["f1", "f2", "f3"],
loop_num: 3
}) YIELD k3
RETURN k3
exec{
algo(k_means).params({
return_id_uuid: "id",
start_ids: ["A", "B", "E"],
k: 3,
distance_type: 1,
node_schema_property: ["f1", "f2", "f3"],
loop_num: 3
}) as k3
return k3
} on my_hdc_graph
Result:
| community | _ids |
|---|---|
| 0 | ["D","B","A","E","K"] |
| 1 | ["J","I"] |
| 2 | ["F","H","C","G"] |
Stream Return
CALL algo.k_means.stream("my_hdc_graph", {
return_id_uuid: "id",
k: 2,
node_schema_property: ["f1", "f2", "f3"],
loop_num: 5
}) YIELD k2
RETURN k2
exec{
algo(k_means).params({
return_id_uuid: "id",
k: 2,
node_schema_property: ["f1", "f2", "f3"],
loop_num: 5
}).stream() as k2
return k2
} on my_hdc_graph
Result:
| community | _ids |
|---|---|
| 0 | ["J","D","B","A","E","K","I"] |
| 1 | ["F","H","C","G"] |

