Overview

LINE (Large-scale Information Network Embedding) is a network embedding model that preserves the local or global network structures. LINE is able to scale to very large, arbitrary types of networks, it was originally proposed in 2015:

• J. Tang, M. Qu, M. Wang, M. Zhang, J. Yan, Q. Zhu, LINE: Large-scale Information Network Embedding (2015)

Concepts

First-order Proximity and Second-order Proximity

First-order proximity in a network shows the local proximity between two nodes, and it is contingent upon connectivity. The existence of a link or a link with a larger weight (negative weight is not considered here) signifies greater first-order proximity among two nodes; if no link exist in-between, their first-order proximity is 0.

On the other hand, second-order proximity between a pair of nodes is the similarity between their neighborhood structure, which is determined through the shared neighbors. In case two nodes lack common neighbors, their second-order proximity is 0.

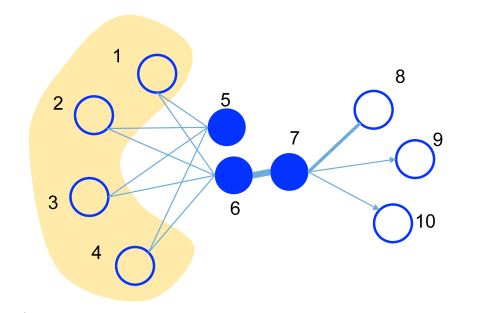
This is an illustrative example, where the edge thickness signifies its weight.

• A substantial weight on the edge between nodes 6 and 7 indicates a high first-order proximity. They shall have close representations in the embedding space.
• Though nodes 5 and 6 are not directly connected, their considerable common neighbors establish a notable second-order proximity. They are expected to be represented closely to each other in the embedding space as well.

LINE Model

The LINE model is designed to embed nodes in graph G = (V,E) into low-dimensional vectors, preserving the first- or second-order proximity between nodes.

LINE with First-order Proximity

To capture the first-order proximity, LINE defines the joint probability for each edge (i,j)∈E connecting nodes v_i and v_j as follows:

where u_i is the low-dimensional vector representation of node v_i. The joint probability p₁ ranges from 0 to 1, with two closer vectors resulting in a higher dot product and, consequently a higher joint probability.

Empirically, the joint probability between node v_i and v_j can be defined as

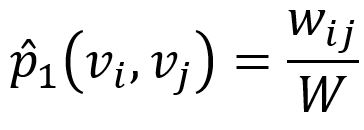
where w_ij denotes the edge weight between nodes v_i and v_j, W is the sum of all edge weights in the graph.

The KL-divergence is adopted to measure the difference between two distributions:

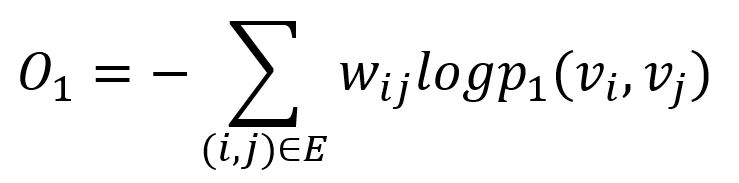
This serves as the objective function that needs to be minimized during training when preserving the first-order proximity.

LINE with Second-order Proximity

To model the second-order proximity, LINE defines two roles for each node - one as the node itself, another as "context" for other nodes (this concept originates from the Skip-gram model). Accordingly, two vector representations are introduced for each node.

For each edge (i,j)∈E, LINE defines the probability of "context" v_j be observed by node v_i as

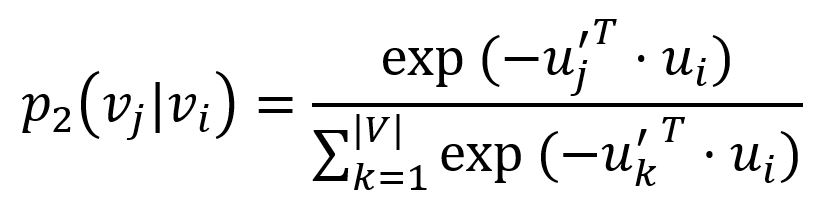
where u'_j is the representation of node v_j when it is regarded as the "context". Importantly, the denominator involves the whole "context" in the graph.

The corresponding empirical probability can be defined as

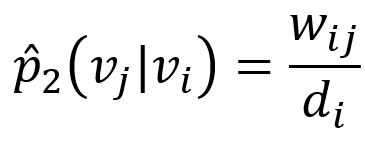
where w_ij is weight of edge (i,j), d_i is the weighted degree of node v_i.

Similarly, the KL-divergence is adopted to measure the difference between two distributions:

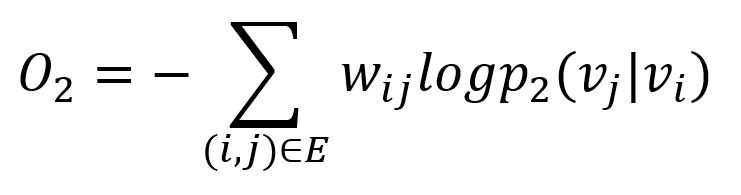
This serves as the objective function that needs to be minimized during training when preserving the second-order proximity.

Model Optimization

Negative Sampling

To improve the computation efficiency, LINE adopts the negative sampling approach which samples multiple negative edges according to some noisy distribution for each edge (i,j). Specifically, the two objective functions are adjusted as:

where σ is the sigmoid function, K is the number of negative edges drawn from the noise distribution P_n(v) ∝ d_v^3/4, d_v is the weighted degree of node v.

Edge-Sampling

Since the edge weights are included in both objectives, these weights will be multiplied into gradients, resulting in the explosion of the gradients and thus compromise the performance. To address this, LINE samples the edges with the probabilities proportional to their weights, and then treat the sampled edges as binary edges for model updating.

Considerations

• The LINE algorithm ignores the direction of edges but calculates them as undirected edges.

Example Graph

To create this graph:

// Runs each row separately in order in an empty graphset
create().edge_property(@default, "score", float)
insert().into(@default).nodes([{_id:"A"},{_id:"B"},{_id:"C"},{_id:"D"},{_id:"E"},{_id:"F"},{_id:"G"},{_id:"H"},{_id:"I"},{_id:"J"}])
insert().into(@default).edges([{_from:"A", _to:"B", score:1}, {_from:"A", _to:"C", score:3}, {_from:"C", _to:"D", score:1.5}, {_from:"D", _to:"F", score:5}, {_from:"E", _to:"C", score:2.2}, {_from:"E", _to:"F", score:0.6}, {_from:"F", _to:"G", score:1.5}, {_from:"G", _to:"J", score:2}, {_from:"H", _to:"G", score:2.5}, {_from:"H", _to:"I", score:1}])

Creating HDC Graph

To load the entire graph to the HDC server hdc-server-1 as hdc_line:

CALL hdc.graph.create("hdc-server-1", "hdc_line", {
  nodes: {"*": ["*"]},
  edges: {"*": ["*"]},
  direction: "undirected",
  load_id: true,
  update: "static",
  query: "query",
  default: false
})

hdc.graph.create("hdc_line", {
  nodes: {"*": ["*"]},
  edges: {"*": ["*"]},
  direction: "undirected",
  load_id: true,
  update: "static",
  query: "query",
  default: false
}).to("hdc-server-1")

Parameters

Algorithm name: line

File Writeback

CALL algo.line.write("hdc_line", {
  params: {
    return_id_uuid: "id",
    edge_schema_property: "score",
    dimension: 3,
    train_total_num: 10,
    train_order: 1,
    learning_rate: 0.01,
    min_learning_rate: 0.0001,
    neg_number: 5,
    resolution: 100
  },
  return_params: {
    file: {
      filename: "embeddings"
    }
  }
})

algo(line).params({
  project: "hdc_line",
  return_id_uuid: "id",
  edge_schema_property: "score",
  dimension: 3,
  train_total_num: 10,
  train_order: 1,
  learning_rate: 0.01,
  min_learning_rate: 0.0001,
  neg_number: 5,
  resolution: 100
}).write({
  file:{
    filename: 'embeddings'
  }
})

_id,embedding_result
J,0.134156,0.147224,-0.127542,
D,-0.110004,0.0445883,0.101143,
F,0.0306388,0.00733918,-0.11945,
H,0.0739559,-0.145214,0.0416526,
B,-0.02514,-0.0317756,-0.110371,
A,-0.0629673,0.0857267,0.100926,
E,0.0989685,0.0532481,0.0514933,
C,-0.127659,-0.136062,0.166552,
I,0.126709,0.103002,-0.0201314,
G,0.134589,-0.0157018,0.0237946,

DB Writeback

Writes the embedding_result values from the results to the specified node property. The property type is float[].

CALL algo.line.write("hdc_line", {
  params: {
    return_id_uuid: "id",
    edge_schema_property: "score",
    dimension: 3,
    train_total_num: 10,
    train_order: 1,
    learning_rate: 0.01,
    min_learning_rate: 0.0001,
    neg_number: 5,
    resolution: 100
  },
  return_params: {
    db: {
      property: "vector"
    }
  }
})

algo(line).params({
  project: "hdc_line",
  return_id_uuid: "id",
  edge_schema_property: "score",
  dimension: 3,
  train_total_num: 10,
  train_order: 1,
  learning_rate: 0.01,
  min_learning_rate: 0.0001,
  neg_number: 5,
  resolution: 100
}).write({
  db: {
      property: "vector"
    }
})

Full Return

CALL algo.line("hdc_line", {
  params: {
    return_id_uuid: "id",
    edge_schema_property: '@default.score',
    dimension: 4,
    train_total_num: 10,
    train_order: 1,
    learning_rate: 0.01,
    min_learning_rate: 0.0001
  },
  return_params: {}
}) YIELD embeddings
RETURN embeddings

exec{
  algo(line).params({
    return_id_uuid: "id",
    edge_schema_property: '@default.score',
    dimension: 4,
    train_total_num: 10,
    train_order: 1,
    learning_rate: 0.01,
    min_learning_rate: 0.0001
  }) as embeddings
  return embeddings
} on hdc_line

Result:

Stream Return

CALL algo.line("hdc_line", {
  params: {
    return_id_uuid: "id",
    edge_schema_property: '@default.score',
    dimension: 3,
    train_total_num: 10,
    train_order: 1,
    learning_rate: 0.01,
    min_learning_rate: 0.0001
  },
  return_params: {
  stream: {}}
}) YIELD embeddings
RETURN embeddings

exec{
  algo(line).params({
    return_id_uuid: "id",
    edge_schema_property: '@default.score',
    dimension: 3,
    train_total_num: 10,
    train_order: 1,
    learning_rate: 0.01,
    min_learning_rate: 0.0001
  }).stream() as embeddings
  return embeddings
} on hdc_line

Result: