Overview
The Minimum Spanning Tree (MST) algorithm computes a spanning tree with the minimum total edge weight for each connected component in a graph.
The MST has a wide range of applications, including network design, clustering, and other optimization problems where minimizing overall cost or weight is essential.
Concepts
Spanning Tree
A spanning tree is a connected subgraph that includes all the nodes of a connected graph G = (V, E) (or of a connected component) and forms a tree (i.e., a graph with no circles). A graph may have multiple spanning trees, but each spanning tree must contain (|V| - 1) edges.
In the example below, the 11 nodes of the graph and the 10 edges highlighted in red form a spanning tree:
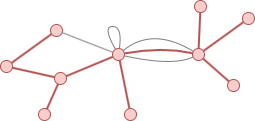
Minimum Spanning Tree (MST)
An MST is a spanning tree with the minimum total sum of edge weights. The construction of an MST begins from a given start node. While the choice of the start node does not affect the correctness of the algorithm, it can influence the structure of the MST and the order in which edges are added. Different start nodes may result in different MSTs, but all of them will be valid MSTs for the given graph.
In the example below, after assigning weights to the edges, three valid MSTs—each starting from a different node—are highlighted in red:
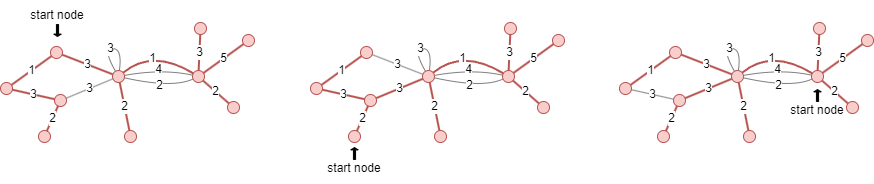
Start Node Selection for MST Computation:
- Each connected component requires only one start node. If multiple start nodes are specified within the same component, only the first one will be used.
- No MST will be computed for any connected component that lacks a specified start node.
- Isolated nodes are not valid as start nodes for MST computation.
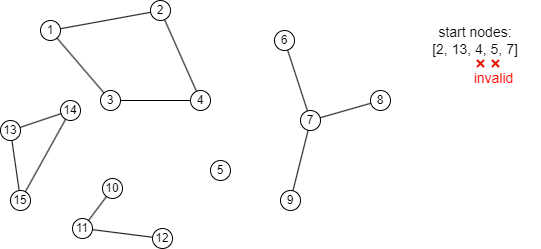
Considerations
- The MST algorithm treats all edges as undirected, ignoring their original direction.
Example Graph

Run the following statements on an empty graph to define its structure and insert data:
ALTER GRAPH CURRENT_GRAPH ADD NODE {
electricCenter (),
village ()
};
ALTER GRAPH CURRENT_GRAPH ADD EDGE {
connects ()-[{distance float}]->()
};
INSERT (A:electricCenter {_id: "A"}),
(B:village {_id: "B"}),
(C:village {_id: "C"}),
(D:village {_id: "D"}),
(E:village {_id: "E"}),
(F:village {_id: "F"}),
(G:village {_id: "G"}),
(H:village {_id: "H"}),
(A)-[:connects {distance: 1}]->(B),
(A)-[:connects {distance: 2.4}]->(C),
(A)-[:connects {distance: 1.2}]->(D),
(A)-[:connects {distance: 0.7}]->(E),
(A)-[:connects {distance: 2.2}]->(F),
(A)-[:connects {distance: 1.6}]->(G),
(A)-[:connects {distance: 0.4}]->(H),
(B)-[:connects {distance: 1.3}]->(C),
(C)-[:connects {distance: 1}]->(D),
(D)-[:connects {distance: 1.65}]->(H),
(E)-[:connects {distance: 1.27}]->(F),
(E)-[:connects {distance: 0.9}]->(G),
(F)-[:connects {distance: 0.45}]->(G);
create().node_schema("electricCenter").node_schema("village").edge_schema("connects");
create().edge_property(@connects, "distance", float);
insert().into(@electricCenter).nodes([{_id:"A"}]);
insert().into(@village).nodes([{_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"}]);
insert().into(@connects).edges([{_from:"A", _to:"B", distance: 1}, {_from:"B", _to:"C", distance: 1.3},{_from:"C", _to:"D", distance: 1}, {_from:"A", _to:"D", distance: 1.2}, {_from:"A", _to:"C", distance: 2.4}, {_from:"D", _to:"H", distance: 1.65}, {_from:"A", _to:"H", distance: 0.4}, {_from:"A", _to:"E", distance: 0.7}, {_from:"A", _to:"F", distance: 2.2}, {_from:"A", _to:"G", distance: 1.6}, {_from:"E", _to:"G", distance: 0.9}, {_from:"E", _to:"F", distance: 1.27}, {_from:"F", _to:"G", distance: 0.45}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: algo(mst)
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
ids |
[]_id |
/ | / | Yes | Specifies the start node by its _id for each connected component; the system will choose the start nodes if it is unset. |
uuids |
[]_uuid |
/ | / | Yes | Specifies the start node by its _uuid for each connected component; the system will choose the start nodes if it is unset. |
edge_schema_property |
[]"<@schema.?><property>" |
/ | / | No | Specifies a numeric edge property used as weight; for each edge, the property’s smallest value is used. Edges without this property are ignored. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results. Edges can only be represented by _uuid; this option is only valid in File Writeback. |
limit |
Integer | ≥-1 | -1 |
Yes | Limits the number of results returned. Set to -1 to include all results. |
File Writeback
CALL algo.mst.write("my_hdc_graph", {
return_id_uuid: "id",
ids: ["A"],
edge_schema_property: "distance"
}, {
file: {
filename: "paths"
}
})
algo(mst).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
ids: ["A"],
edge_schema_property: "distance"
}).write({
file: {
filename: "paths"
}
})
Result:
A--[107]--H
A--[108]--E
E--[111]--G
F--[113]--G
A--[101]--B
A--[104]--D
C--[103]--D
Full Return
CALL algo.mst.run("my_hdc_graph", {
ids: ["A"],
edge_schema_property: "@connects.distance"
}) YIELD mst
RETURN mst
exec{
algo(mst).params({
ids: ["A"],
edge_schema_property: "@connects.distance"
}) as mst
return mst
} on my_hdc_graph
Result:
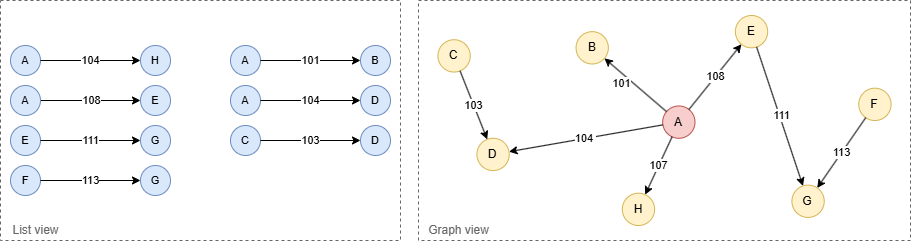
Stream Return
CALL algo.mst.stream("my_hdc_graph", {
ids: ["A"],
edge_schema_property: "distance"
}) YIELD mst
FOR e1 IN pedges(mst)
MATCH ()-[e2 WHERE e2._uuid = e1._uuid]->()
RETURN sum(e2.distance)
exec{
algo(mst).params({
ids: ["A"],
edge_schema_property: "distance"
}).stream() as mst
uncollect pedges(mst) as e1
find().edges({_uuid == e1._uuid}) as e2
return sum(e2.distance)
} on my_hdc_graph
Result: 5.65

