The Skip-gram (SG) model is a widely used method for generating word embeddings in natural language processing (NLP). Its underlying principles have also been used in graph embedding algorithms such as Node2Vec and Struc2Vec to produce node embeddings.
Background
The Skip-gram model originated from the Word2Vec algorithm, which was introduced by T. Mikolov et al. introduced Word2Vec at Google in 2013. Word2Vec maps words into a vector space such that semantically similar words are represented by vectors that lie close to each other.
- T. Mikolov, K. Chen, G. Corrado, J. Dean, Efficient Estimation of Word Representations in Vector Space (2013)
- X. Rong, word2vec Parameter Learning Explained (2016)
In the realm of graph embedding, the introduction of DeepWalk in 2014 marked a pivotal moment, applying the Skip-gram model to generate vector representations of nodes in a graph. The key idea is to treat nodes as "words", and the sequences of nodes generated by random walks as "sentences" forming a "corpus".
- B. Perozzi, R. Al-Rfou, S. Skiena, DeepWalk: Online Learning of Social Representations (2014)
Subsequent graph embedding methods such as Node2Vec and Struc2Vec have enhanced the DeepWalk approach, while still relying on the Skip-gram framework.
To better understand the Skip-gram model, we will illustrate it in its original context within natural language processing.
Model Overview
The core idea behind the Skip-gram model is to predict surrounding context words given a target word. As illustrated in the diagram below, the input word, denoted as , is fed into the model. The model then predicts a set of nearby context words related to : , , , and . Here, the symbols / signify the words that appear before and after the target word in the sequence. The number of context words can be adjusted as needed.
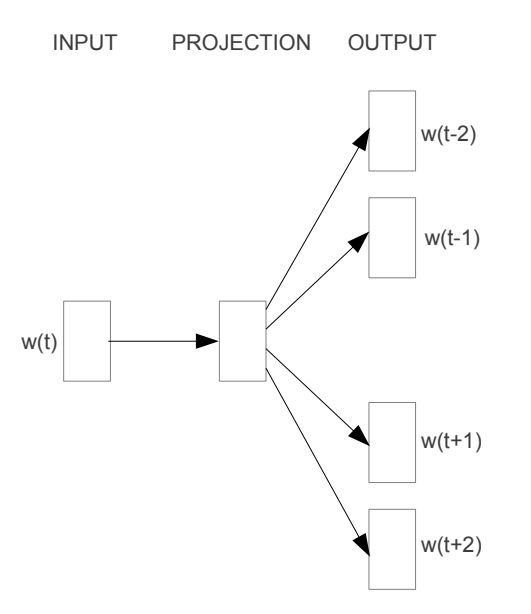
However, it's important to recognize that the ultimate goal of the Skip-gram model is not the prediction task itself. Rather, its primary objective is to derive the weight matrix found within the mapping relationship (indicated as PROJECTION in the diagram), which serves as the learned vector representations of words.
Corpus
A corpus is a collection of sentences or texts that a model utilizes to learn the semantic relationships between words.
For example, consider a vocabulary containing 10 distinct words extracted from a corpus: graph, is, a, good, way, to, visualize, data, very, at.
These words can be used to construct sentences such as:
Graph is a good way to visualize data.
Sliding Window Sampling
The Skip-gram model uses a sliding window sampling technique to generate training samples. This method involves a "window" that moves sequentially over each word in a sentence. For each target word, the model pairs it with context words that appear within a predefined range, denoted as window_size, both before and after the target.
Below is an illustration of the sampling process when window_size.
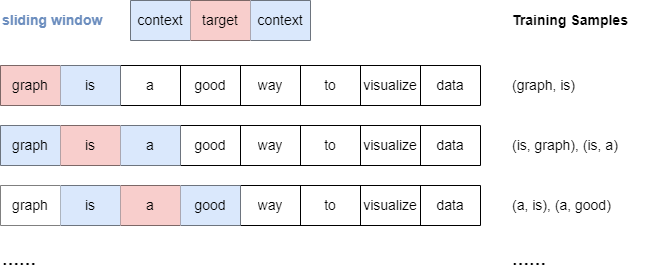
It's important to note that when window_size, all context words within the specified window are treated equally, regardless of their distance from the target word.
One-hot Encoding
Since words are not directly interpretable by machine learning models, they must be converted into machine-understandable representations.
One common method for encoding words is one-hot encoding. In this approach, each word is represented by a unique binary vector where only one element is "hot" (set to ) and all others are "cold" (set to ). The position of the in the vector corresponds to the index of the word in the vocabulary.
Below is an example of how one-hot encoding is applied to our vocabulary:
| Word | One-hot Encoded Vector |
|---|---|
| graph | |
| is | |
| a | |
| good | |
| way | |
| to | |
| visualize | |
| data | |
| very |
Skip-gram Architecture

The architecture of the Skip-gram model is illustrated above, where:
- is the one-hot encoded input vector of the target word, and is the number of words in the vocabulary.
- is the weight matrix mapping from the input layer to the hidden layer, where is the embedding dimension.
- is the hidden layer vector.
- is the weight matrix from the hidden layer to the output layer. Note that is not the transpose of —they are distinct matrices.
- is the vector before applying the activation function Softmax.
- () are the final output vectors (also referred to as panels). panels correspond to the context words predicted from the target word.
Softmax: The Softmax function serves as an activation function that transforms a vector of real numbers into a probability distribution vector. In the resulting vector, all elements sum to . The formula for Softmax is as follows:
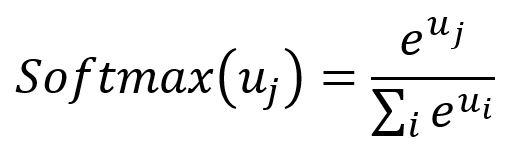
Forward Propagation
In our example, let , and set . We begin by randomly initializing the weight matrices and as shown below. For demonstration, we will use the sample pairs (is, graph) and (is, a).
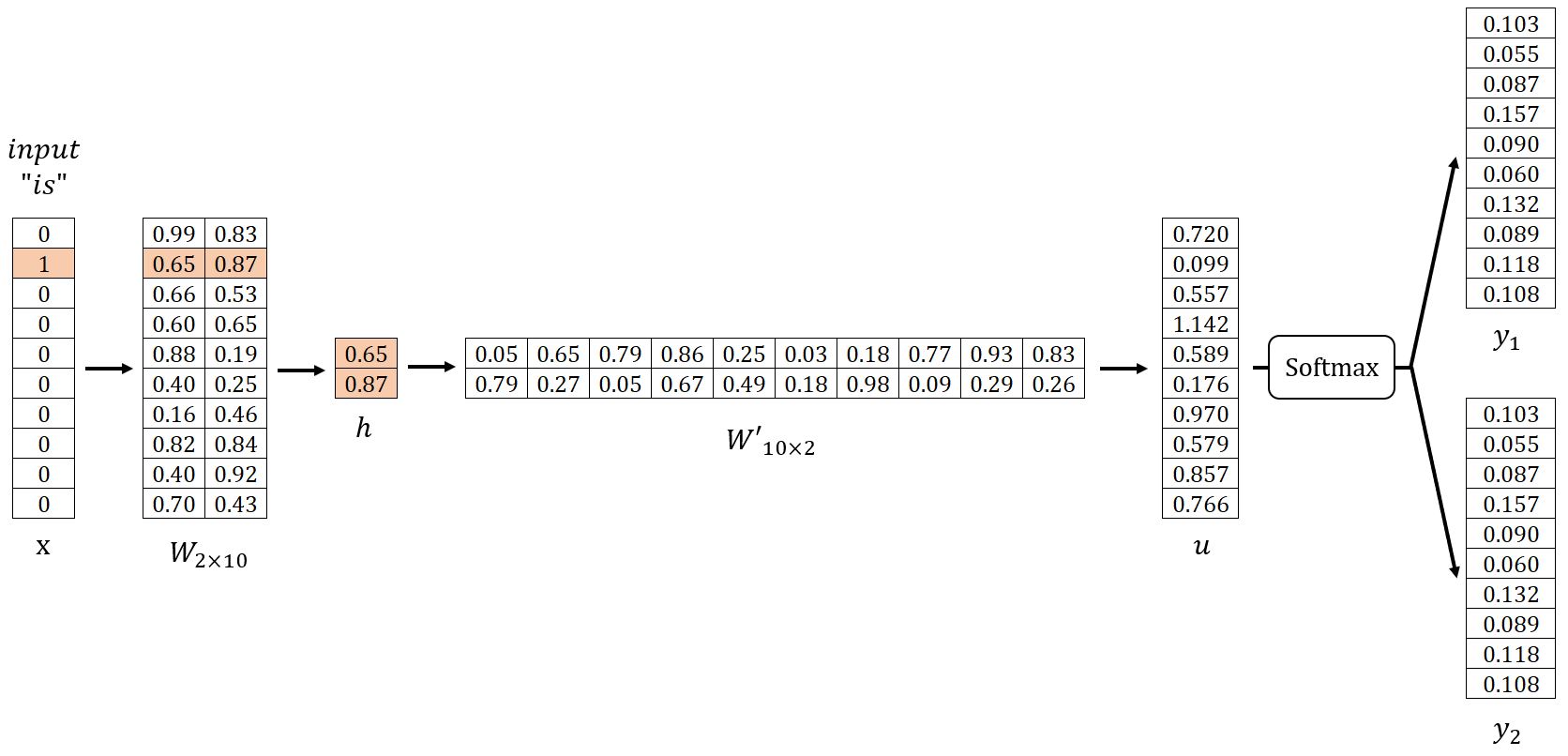
Input Layer → Hidden Layer
Get the hidden layer vector by:
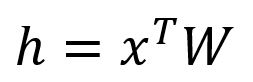
Given that is a one-hot encoded vector with only , corresponds to the -th row of the matrix . This operation is essentially a simple lookup process:
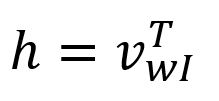
where is the input vector of the target word.
In fact, each row of the matrix , denoted as , is viewed as the final embedding of each word in the vocabulary.
Hidden Layer → Output Layer
Get the vector by:
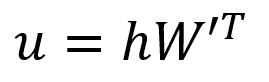
The -th component of the vector is computed as the dot product between the vector and the transpose of the -th column vector of the matrix :
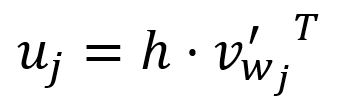
where is the output vector of the -th word in the vocabulary.
In the Skip-gram model, each word in the vocabulary has two distinct representations: the input vector and the output vector . The input vector represents the word when it is used as the target, while the output vector represents the word when it acts as a context word.
During computation, is essentially the dot product of the input vector of the target word and the output vector of the -th word . The Skip-gram model is built on the principle that a higher similarity between two vectors yields a larger dot product between them.
It is also important to note that only the input vectors are ultimately used as the word embeddings. Separating input and output vectors simplifies the computation process, improving both efficiency and accuracy during training and inference.
Get each output panel by:

where is the -th component of , representing the probability of the -th word within the vocabulary being predicted while considering the given target word. Apparently, the sum of all probabilities is .
The words with the highest predicted probabilities are selected as the context words. In our example, where , the predicted context words are good and visualize.

Backpropagation
SGD is used to backpropagate the errors and adjust the weights in both and .
Loss Function
Our goal is to maximize the probabilities of the context words, which is equivalent to maximizing the product of these probabilities:
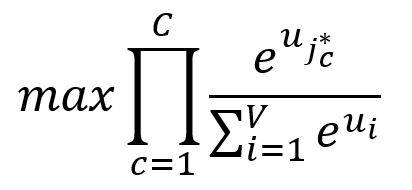
where is the index of the expected -th output context word.
Because minimizing a function is often more straightforward and practical than maximizing it, we transform the above objective accordingly:
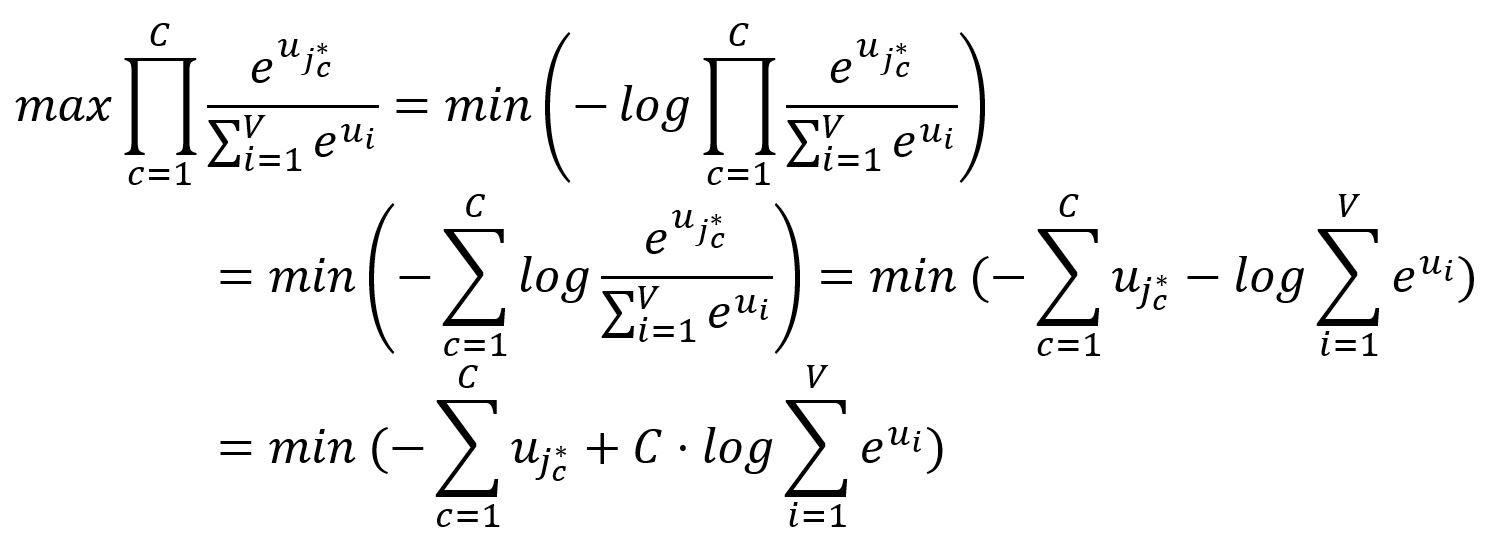
Therefore, the loss function for the Skip-gram model is defined as:
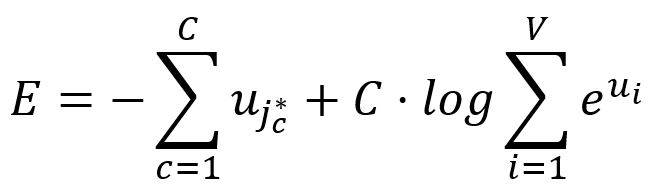
Take the partial derivative of with respect to :
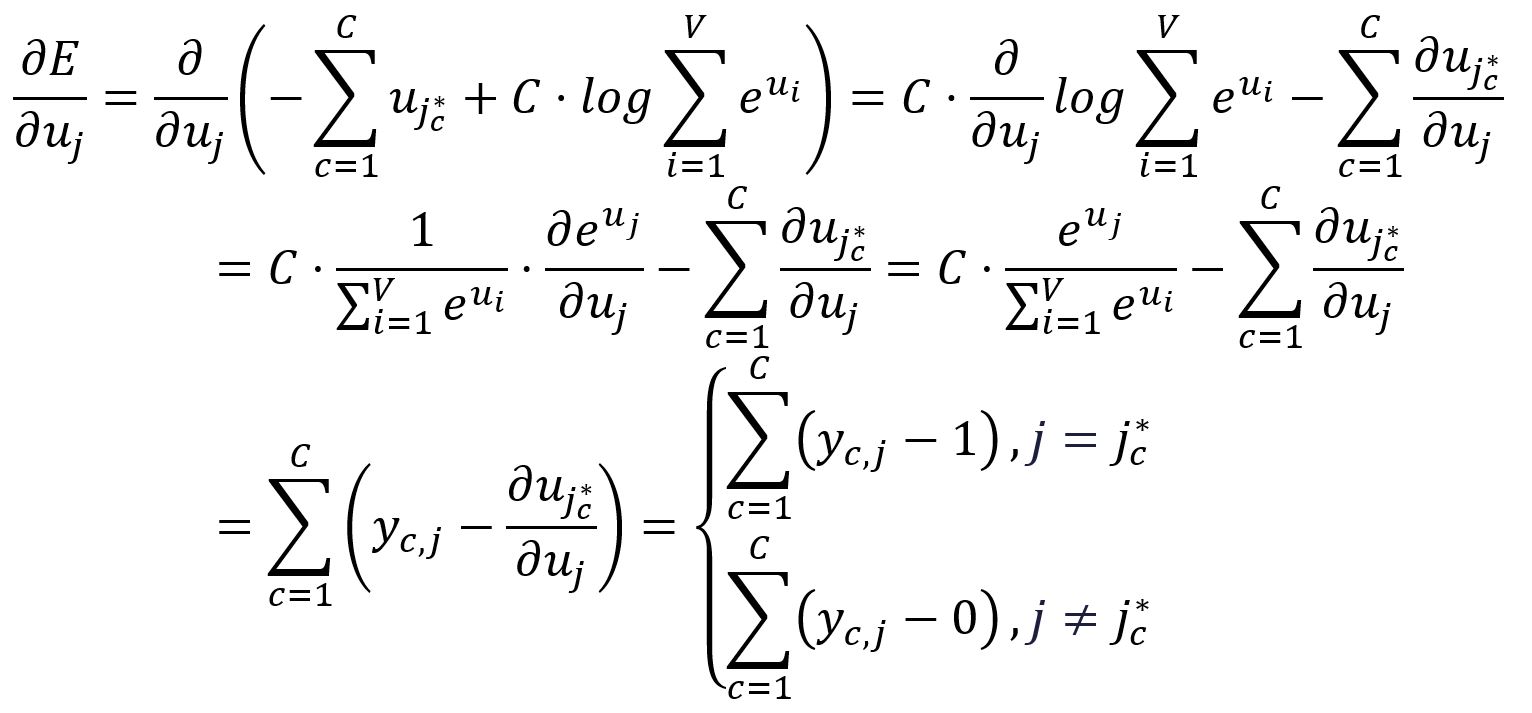
To simplify the notaion going forward, we define the following:

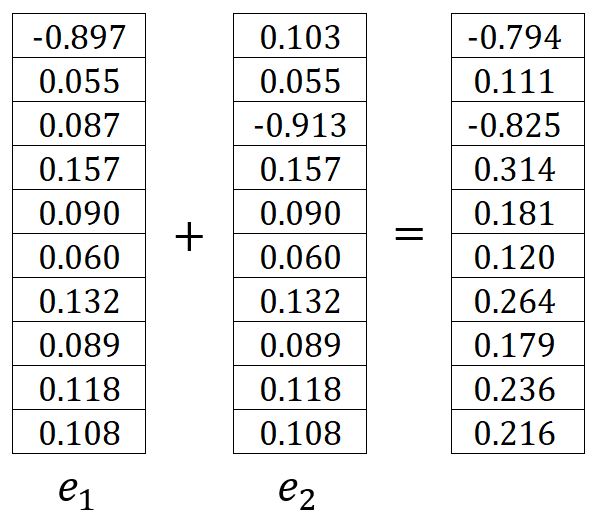
where is the one-hot encoding vector of the -th expected output context word. In our example, and are the one-hot encoded vectors of the words graph and a, respectively. Therefore, the corresponding errors and are calculated as follows:

Therefore, can be written as:
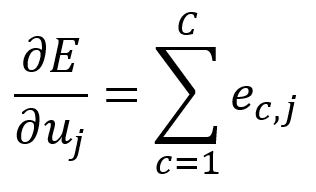
In our example, it is calculated as:
Output Layer → Hidden Layer
Adjustments are applied to all the weights in matrix , meaning that the output vectors of all words are updated.
Calculate the partial derivative of with respect to :
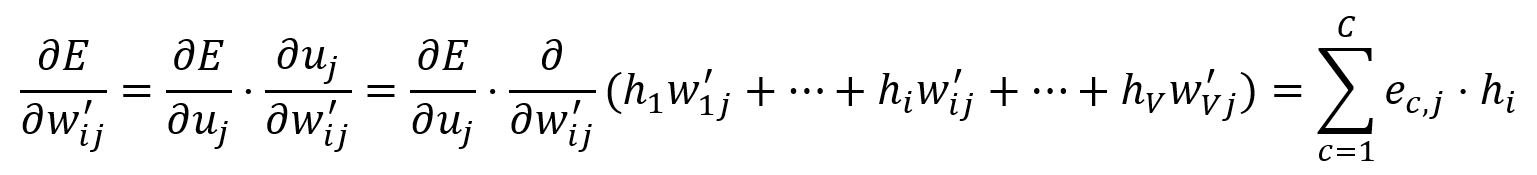
Adjust according to the learning rate :
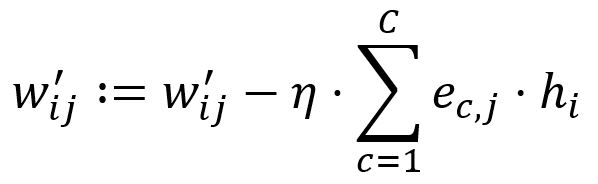
Set . For instance, and are updated to:
Hidden Layer → Input Layer
Only the weights in matrix corresponding to the input vector of the target word are updated.
The vector is obtained by only looking up the -th row of matrix (given that ):
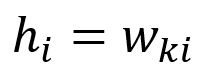
Calculate the partial derivative of with respect to :
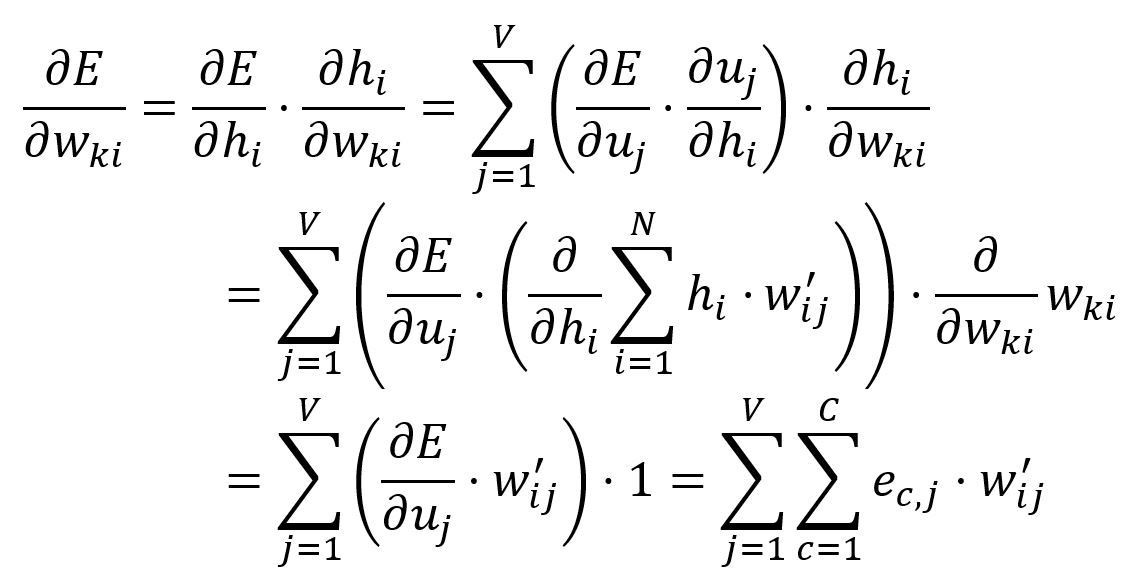
Adjust according to the learning rate :
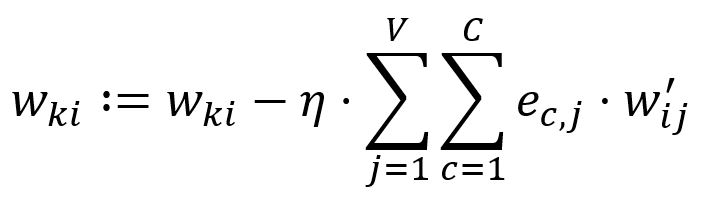
In our example, , hence, and are updated:
Optimization
We have explored the fundamentals of the Skip-gram model. However, incorporating optimizations is essential to keep the model's computational complexity practical for real-world applications. Click here to continue reading.

