La rétropropagation (ou BP, pour Backward Propagation) est une technique fondamentale utilisée dans la formation de modèles pour les embeddings de graphes.
L'algorithme BP comprend deux étapes principales :
- Propagation avant : Les données d'entrée sont introduites dans la couche d'entrée d'un réseau de neurones ou modèle. Elles passent ensuite par une ou plusieurs couches cachées avant de générer une sortie à partir de la couche de sortie.
- Rétropropagation : La sortie générée est comparée à la valeur réelle ou attendue. Ensuite, l'erreur est transmise de la couche de sortie à travers les couches cachées jusqu'à la couche d'entrée. Durant ce processus, les poids du modèle sont ajustés à l'aide de la technique de descente de gradient.
Les ajustements itératifs des poids constituent le processus d'apprentissage du réseau de neurones. Nous allons expliquer davantage avec un exemple concret.
Préparations
Réseau de Neurones
Les réseaux de neurones sont généralement composés de plusieurs composants essentiels : une couche d'entrée, une ou plusieurs couches cachées, et une couche de sortie. Voici un exemple simple d'architecture de réseau de neurones :
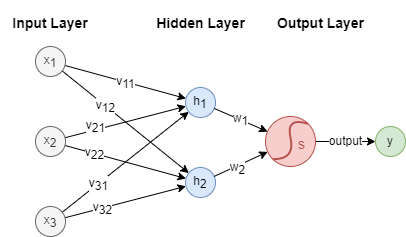
Dans cette illustration, est le vecteur d'entrée contenant 3 caractéristiques, est la sortie. Nous avons deux neurones et dans la couche cachée. La fonction d'activation sigmoïde est appliquée dans la couche de sortie.
De plus, les connexions entre les couches sont caractérisées par les poids : ~ sont les poids entre la couche d'entrée et la couche cachée, et sont les poids entre la couche cachée et la couche de sortie. Ces poids sont essentiels dans les calculs effectués au sein du réseau de neurones.
Fonction d'Activation
Les fonctions d'activation permettent au réseau de neurones d'effectuer une modélisation non linéaire. Sans fonctions d'activation, le modèle ne peut exprimer que des mappings linéaires, limitant ainsi leur capacité. Une large gamme de fonctions d'activation existe, chacune servant un objectif unique. La fonction sigmoïde utilisée dans ce contexte est décrite par la formule et le graphique suivants :
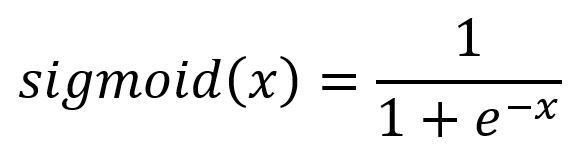
Poids Initiaux
Les poids sont initialisés avec des valeurs aléatoires. Supposons que les poids initiaux soient les suivants :

Échantillons d'Entraînement
Considérons trois ensembles d'échantillons d'entraînement comme indiqué ci-dessous, où l'exposant indique l'ordre de l'échantillon :
- Entrées : , ,
- Sorties : , ,
L'objectif principal du processus de formation est d'ajuster les paramètres du modèle (poids) afin que la sortie prédite/calculée () s'aligne étroitement avec la sortie réelle () lorsqu'on lui fournit l'entrée ().
Propagation Avant
Couche d'Entrée → Couche Cachée
Les neurones et sont calculés par :
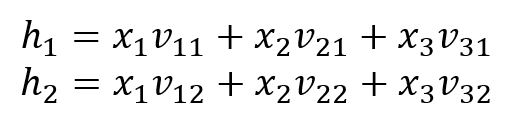
Couche Cachée → Couche de Sortie
La sortie est calculée par :
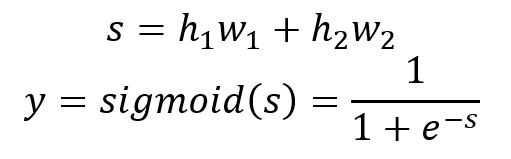
Voici le calcul des 3 échantillons :
| 2.4 | 1.8 | 2.28 | 0.907 | 0.64 | |
| 0.75 | 1.2 | 0.84 | 0.698 | 0.52 | |
| 1.35 | 1.4 | 1.36 | 0.796 | 0.36 |
Apparemment, les trois sorties calculées () sont très différentes de celles attendues ().
Rétropropagation
Fonction de Perte
Une fonction de perte est utilisée pour quantifier l'erreur ou la disparité entre les sorties du modèle et les sorties attendues. Elle est aussi appelée fonction objectif ou fonction de coût. Utilisons ici l'erreur quadratique moyenne (MSE) comme fonction de perte :
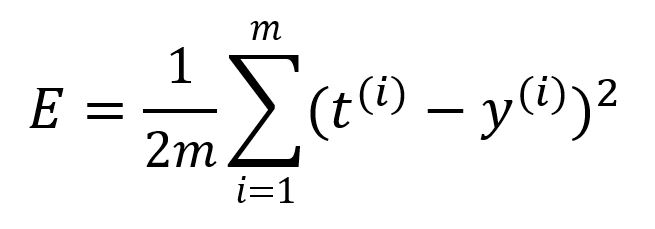
où est le nombre d'échantillons. Calculez l'erreur de cette série de propagation avant ainsi :
Une valeur plus petite de la fonction de perte correspond à une plus grande précision du modèle. L'objectif fondamental de la formation du modèle est de minimiser la valeur de la fonction de perte le plus possible.
Considérez les entrées et sorties comme des constantes, tout en s'intéressant aux poids en tant que variables au sein de la fonction de perte. L'objectif est donc d'ajuster les poids de manière à obtenir la plus faible valeur de la fonction de perte - c'est là que la technique de la descente de gradient entre en jeu.
Dans cet exemple, la descente de gradient par lot (BGD) est utilisée, c'est-à-dire que tous les échantillons sont impliqués dans le calcul du gradient. Fixez le taux d'apprentissage .
Couche de Sortie → Couche Cachée
Ajustez les poids et respectivement.
Calculez la dérivée partielle de par rapport à avec la règle de chaîne:
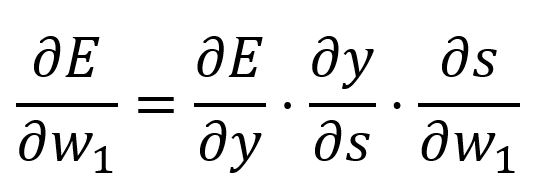
où,
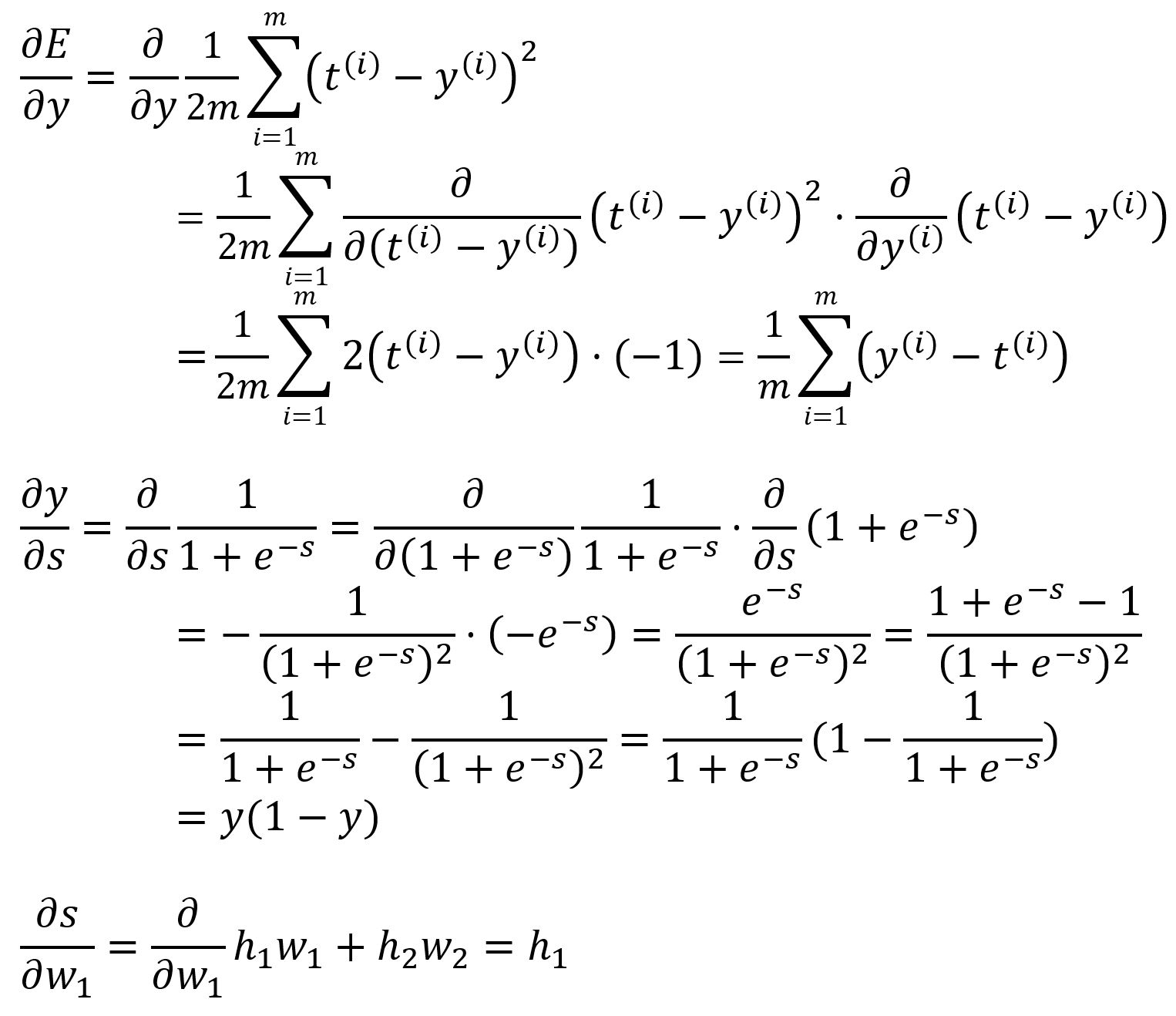
Calculez avec les valeurs :
Alors,
Étant donné que tous les échantillons sont impliqués dans le calcul de la dérivée partielle, lors du calcul de et , nous prenons la somme de ces dérivées sur tous les échantillons et obtenons ensuite la moyenne.
Donc, est mis à jour de .
Le poids peut être ajusté de manière similaire en calculant la dérivée partielle de par rapport à . Dans cette ronde, est mis à jour de à .
Couche Cachée → Couche d'Entrée
Ajustez les poids ~ respectivement.
Calculez la dérivée partielle de par rapport à avec la règle de chaîne:
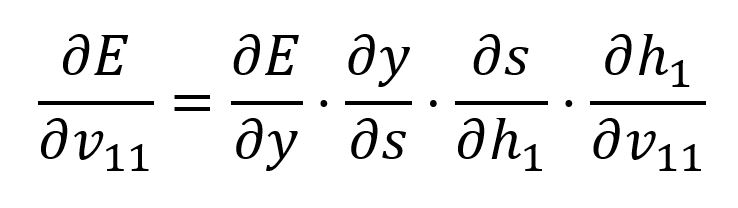
Nous avons déjà calculé et , ci-dessous sont les deux suivants :
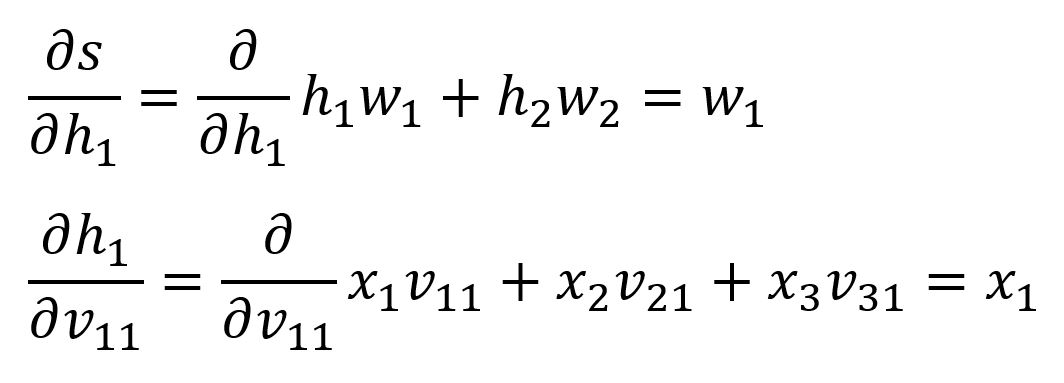
Calculez avec les valeurs :
Alors, .
Donc, est mis à jour à .
Les poids restants peuvent être ajustés de manière similaire en calculant la dérivée partielle de par rapport à chacun d'eux. Dans cette ronde, ils sont mis à jour comme suit :
- est mis à jour de à
- est mis à jour de à
- est mis à jour de à
- est mis à jour de à
- est mis à jour de à
Itérations d'Entraînement
Appliquez les poids ajustés au modèle et procédez à la propagation avant en utilisant les mêmes trois échantillons. Dans cette itération, l'erreur résultante est réduite à .
L'algorithme de rétropropagation effectue de manière itérative les étapes de propagation avant et de rétropropagation pour entraîner le modèle. Ce processus continue jusqu'à ce que le nombre d'entraînements désigné ou la limite de temps soit atteinte, ou lorsque l'erreur diminue jusqu'à un seuil prédéfini.

