Vue d’ensemble
La traversée de graph est une technique de recherche utilisée pour visiter et explorer systématiquement tous les nodes d'un graph. L'objectif principal de la traversée de graph est de découvrir et d'examiner la structure et les connexions du graph. Il existe deux stratégies courantes de traversée de graph :
- Recherche en largeur (BFS)
- Recherche en profondeur (DFS)
L'algorithme de Recherche en largeur (BFS) explore un graph couche par couche et suit ces étapes :
- Créer une file d'attente (premier entré, premier sorti) pour suivre les nodes visités.
- Commencer à partir d'un node sélectionné, l'enfiler dans la file d'attente et le marquer comme visité.
- Défiler un node depuis l'avant de la file d'attente, enfiler tous ses voisins non visités dans la file d'attente et les marquer comme visités.
- Répéter l'étape 3 jusqu'à ce que la file d'attente soit vide.
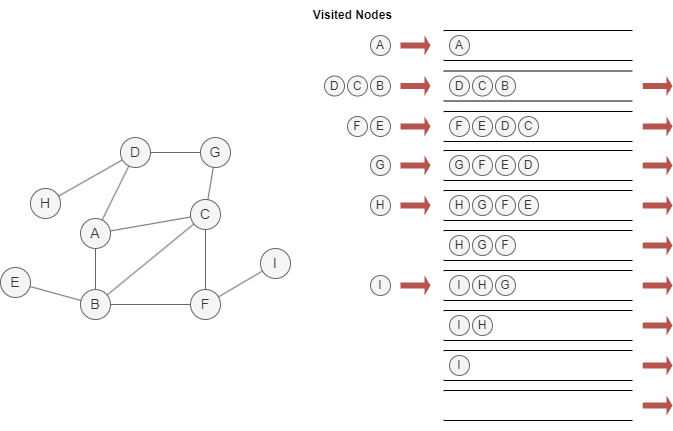
Ci-dessous un exemple de traversée du graph en utilisant l'approche BFS, en commençant par le node A et en supposant visiter les voisins par ordre alphabétique (A~Z) :
Considerations
- Seuls les nodes qui sont dans le même composant connecté que le node de départ peuvent être traversés. Les nodes dans différents composants connectés ne seront pas inclus dans les résultats de la traversée.
Syntaxe
- Commande :
algo(traverse) - Paramètres :
Nom |
Type |
Spec |
Par défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| ids / uuids | _id / _uuid |
/ | / | Non | ID/UUID du node de départ pour traverser le graph |
| direction | string | in, out |
/ | Oui | Direction des edges lors de la traversée du graph |
| traverse_type | string | bfs |
bfs |
Oui | Pour traverser le graph selon l'approche BFS, gardez-le en bfs |
Exemples
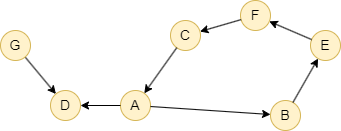
File Writeback
Spécification |
Contenu |
Description |
|---|---|---|
| filename | _id,_id |
Le node visité (toNode), et le node à partir duquel il est visité (fromNode) |
algo(traverse).params({
ids: ['A'],
direction: 'out',
traverse_type: 'bfs'
}).write({
file: {
filename: 'result'
}
})
Résultats : Fichier result
F,E
E,B
D,A
C,F
B,A
A,A

