Vue d’ensemble
Le problème de plus court chemin à source unique (SSSP) est de calculer, pour chaque node atteignable depuis le node source, le chemin le plus court avec le poids total de edge minimum parmi tous les chemins possibles ; ou dans le cas des graphs non pondérés, le chemin le plus court avec le nombre minimum de edges. Le coût (ou la distance) du plus court chemin est le poids total des edges ou le nombre de edges.
L'algorithme Delta-Stepping peut être considéré comme une variante de l'algorithme de Dijkstra avec son potentiel de parallélisme.
Matériel connexe de l'algorithme :
- U. Meyer, P.Sanders, Δ-Stepping: A Parallel Single Source Shortest Path Algorithm (1998)
Concepts
Delta-Stepping Single-Source Shortest Path
L'algorithme Delta-Stepping Single-Source Shortest Path (SSSP) introduit le concept de "buckets" et effectue des opérations de relaxation de manière plus grossière. L'algorithme utilise un paramètre nombre réel positif delta (Δ) pour accomplir ce qui suit :
- Maintenir un tableau B de buckets tel que B[i] contient des nodes dont la distance est comprise dans l'intervalle [iΔ, (i+1)Δ). Ainsi, Δ est également appelé la "largeur de pas" ou "largeur de bucket".
- Distinguer entre les light edges de poids ≤ Δ et les heavy edges de poids > Δ dans le graph. Les nodes des light edges sont prioritaires lors de la relaxation car ils ont des poids plus faibles et sont plus susceptibles d'offrir des chemins plus courts.
Le terme relaxation fait référence au processus de mise à jour de la distance d'un node v connecté au node u à une distance potentiellement plus courte en considérant le chemin via le node u. Plus précisément, la distance du node v est mise à jour à dist(v) = dist(u) + w(u,v), où w(u,v) est le poids du edge (u,v). Cette mise à jour est effectuée uniquement si la dist(v) actuelle est supérieure à dist(u) + w(u,v).
Dans l'algorithme Delta-Stepping SSSP, la relaxation inclus également l'assignation du node relaxé au bucket correspondant basé sur sa valeur de distance mise à jour.
Voici la description de base de l'algorithme Delta-Stepping SSSP, accompagnée d'un exemple pour calculer les chemins les plus courts pondérés dans un graph non orienté à partir de la node source b, et Δ est fixé à 3 :
1. Au début de l'algorithme, tous les nodes ont une distance infinie sauf le node source qui est à 0. Le node source est assigné au bucket B[0].
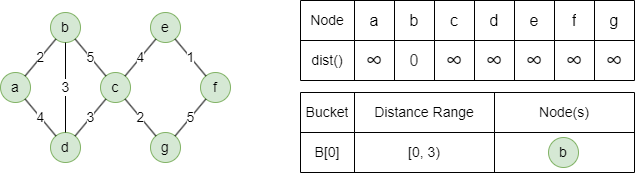
2. À chaque itération, retirer tous les nodes du premier bucket non vide B[i]:
- Relaxer tous les voisins light-edge des nodes retirés, les nodes relaxés pourraient être assignés à B[i] ou B[i+1]; différer la relaxation des voisins heavy-edge.
- Si B[i] est re-rempli, répéter l'opération ci-dessus jusqu'à ce que B[i] soit vide.
- Relaxer tous les voisins heavy-edge différés.

Relaxer les voisins light-edge a avec dist(a) = min(0+2,∞) = 2, et d avec dist(b) = min(0+3,∞) = 3.

Le voisin light-edge b ne peut être relaxé.
Relaxer le voisin heavy-edge c avec dist(c) = min(0+5,∞) = 5, d ne peut être relaxé.
3. Répéter l'étape 2 jusqu'à ce que tous les buckets soient vides.
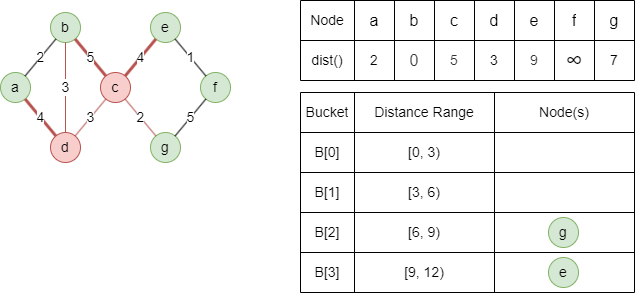
Relaxer le voisin light-edge g avec dist(g) = min(5+2,∞) = 7, b, c et d ne peuvent être relaxés.
Relaxer le voisin heavy-edge e avec dist(e) = min(5+4,∞) = 9, a et b ne peuvent être relaxés.
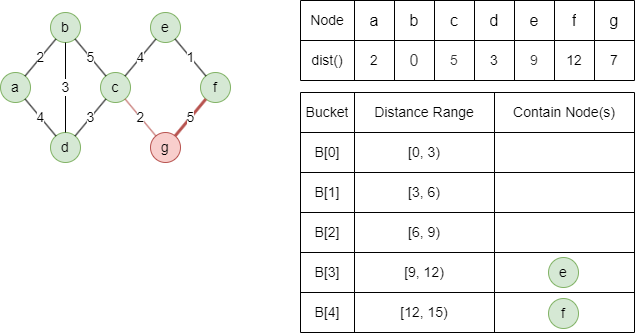
Le voisin light-edge c ne peut être relaxé.
Relaxer le voisin heavy-edge f avec dist(f) = min(7+5,∞) = 12.
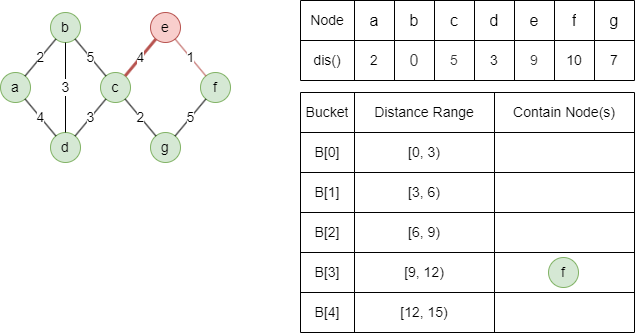
Relaxer le voisin light-edge f avec dist(f) = min(9+1,12) = 10.
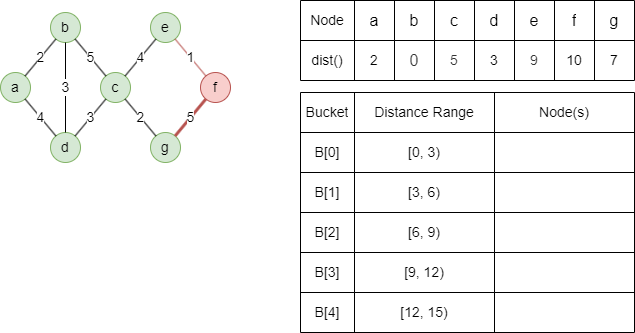
Le voisin light-edge e ne peut être relaxé.
Le voisin heavy-edge g ne peut être relaxé.
L'algorithme se termine ici car tous les buckets sont vides.
En divisant les nodes en buckets et en les traitant en parallèle, l'algorithme Delta-Stepping peut exploiter les ressources informatiques disponibles plus efficacement, ce qui le rend adapté aux graphs de grande échelle et aux environnements de calcul parallèle.
Considérations
- L'algorithme Delta-Stepping SSSP n'est applicable qu'aux graphs avec des poids de edges non négatifs. Si des poids négatifs sont présents, l'algorithme Delta-Stepping SSSP pourrait produire de faux résultats. Dans ce cas, un autre algorithme comme le SPFA devrait être utilisé.
- Si plusieurs plus courts chemins existent entre deux nodes, tous seront trouvés.
- Dans les graphs déconnectés, l'algorithme n'affiche que les plus courts chemins depuis le node source vers tous les nodes appartenant à la même composante connectée que le node source.
Syntaxe
- Commande :
algo(sssp) - Paramètres :
Nom |
Type |
Spécifications |
Par défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| ids / uuids | _id / _uuid |
/ | / | Non | ID/UUID du node source unique |
| direction | string | in, out |
/ | Oui | Direction du plus court chemin, ignorer la direction de edge si non spécifié |
| edge_schema_property | []@schema?.property |
Type numérique, doit être LTE | / | Oui | Une ou plusieurs propriétés de edge à utiliser comme poids de edge, où les valeurs de plusieurs propriétés sont additionnées ; traiter le graph comme non pondéré si non spécifié |
| record_path | int | 0, 1 |
0 |
Oui | 1 pour retourner les plus courts chemins, 0 pour retourner les distances les plus courtes |
| sssp_type | string | delta_stepping |
dijkstra |
Non | Pour exécuter l'algorithme Delta-Stepping SSSP, le garder comme delta_stepping |
| delta | float | >0 | 2 |
Oui | La valeur de delta |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
| order | string | asc, desc |
/ | Oui | Trier les nodes par la distance la plus courte depuis le node source |
Exemples
Le graph d'exemple est le suivant :
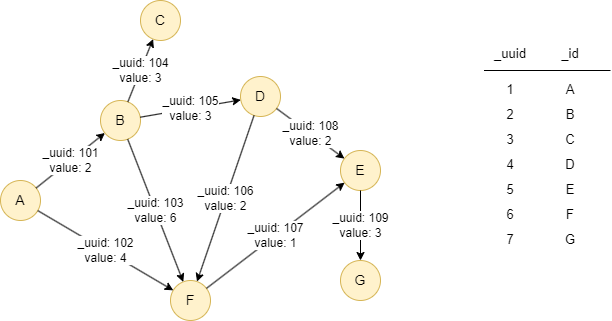
File Writeback
| Spécification | record_path |
Contenu | Description |
|---|---|---|---|
| nom de fichier | 0 | _id,totalCost |
La distance/coût le plus court du node source vers chaque autre node |
| 1 | _id--_uuid--_id |
Le plus court chemin du node source vers chaque autre node, le chemin est représenté par l'ID alternatif de nodes et l'UUID de edges qui forment le chemin |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'delta_stepping',
delta: 2
}).write({
file: {
filename: 'costs'
}
})
Résultats : Fichier costs
G,8
F,4
E,5
D,5
C,5
B,2
A,0
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'delta_stepping',
delta: 2,
record_path: 1
}).write({
file: {
filename: 'paths'
}
})
Résultats : Fichier paths
A--[102]--F--[107]--E--[109]--G
A--[102]--F--[107]--E
A--[101]--B--[105]--D
A--[101]--B--[104]--C
A--[102]--F
A--[101]--B
A
Direct Return
| Alias Ordinal | record_path |
Type | Description | Colonnes |
|---|---|---|---|---|
| 0 | 0 | []perNode | Le coût/distance le plus court du node source vers chaque autre node | _uuid, totalCost |
| 1 | []perPath | Le plus court chemin du node source vers chaque autre node, le chemin est représenté par l'UUID alternatif de nodes et l'UUID de edges qui forment le chemin | / |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'delta_stepping',
delta: 2,
order: 'desc'
}) as costs
return costs
Résultats : costs
| _uuid | totalCost |
|---|---|
| 7 | 8 |
| 5 | 5 |
| 4 | 5 |
| 3 | 5 |
| 6 | 4 |
| 2 | 2 |
| 1 | 0 |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
direction: 'out',
record_path: 1,
sssp_type: 'delta_stepping',
delta: 2,
order: 'asc'
}) as paths
return paths
Résultats : paths
| 1 |
| 1--[101]--2 |
| 1--[102]--6 |
| 1--[102]--6--[107]--5 |
| 1--[101]--2--[105]--4 |
| 1--[101]--2--[104]--3 |
| 1--[102]--6--[107]--5--[109]--7 |
Stream Return
| Alias Ordinal | record_path |
Type | Description | Colonnes |
|---|---|---|---|---|
| 0 | 0 | []perNode | Le coût/distance le plus court du node source vers chaque autre node | _uuid, totalCost |
| 1 | []perPath | Le plus court chemin du node source vers chaque autre node, le chemin est représenté par l'UUID alternatif de nodes et l'UUID de edges qui forment le chemin | / |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'delta_stepping'
}).stream() as costs
where costs.totalCost <> [0,5]
return costs
Résultats : costs
| _uuid | totalCost |
|---|---|
| 6 | 4 |
| 2 | 2 |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'delta_stepping',
record_path: 1
}).stream() as p
where length(p) <> [0,3]
return p
Résultats : p
| 1--[102]--6--[107]--5 |
| 1--[101]--2--[105]--4 |
| 1--[101]--2--[104]--3 |
| 1--[102]--6 |
| 1--[101]--2 |

