Vue d’ensemble
Le problème du plus court chemin à source unique (SSSP) consiste à calculer, pour chaque node accessible depuis le node source, le chemin le plus court avec le poids total minimal des edges parmi tous les chemins possibles ; ou dans le cas des graph non pondérés, le chemin le plus court avec le nombre minimal d'edges. Le coût (ou la distance) du chemin le plus court est le poids total des edges ou le nombre d'edges.
L'algorithme original de Dijkstra a été conçu par le scientifique en informatique néerlandais Edsger W. Dijkstra en 1956 pour trouver le plus court chemin entre deux nodes donnés. Le plus court chemin à source unique est une variante courante, facilitant la planification efficace des chemins et l'analyse des réseaux.
Concepts
Plus Court Chemin à Source Unique de Dijkstra
Voici l'implémentation de base de l'algorithme de Plus Court Chemin à Source Unique de Dijkstra, accompagnée d'un exemple pour calculer les chemins les plus courts pondérés dans un graph non orienté à partir du node source b :
1. Créer une file de priorité pour stocker les nodes et leurs distances correspondantes par rapport au node source. Initialiser la distance du node source à 0 et les distances de tous les autres nodes à l'infini. Tous les nodes sont marqués comme non visités.

2. Extraire le node avec la distance minimale de la file et le marquer comme visité, relaxer tous ses voisins non visités.

dist(a) = min(0+2,∞) = 2, dist(c) = min(0+1,∞) = 1
Le terme relaxation fait référence au processus de mise à jour de la distance d'un node v connecté au node u vers une distance potentiellement plus courte en considérant le chemin via le node u. Plus précisément, la distance du node v est mise à jour à dist(v) = dist(u) + w(u,v), où w(u,v) est le poids de l'edge (u,v). Cette mise à jour est effectuée uniquement si la distance actuelle dist(v) est supérieure à dist(u) + w(u,v).
Une fois qu'un node a été marqué comme visité, son chemin le plus court a été fixé et sa distance ne changera plus pendant le reste de l'algorithme. L'algorithme ne met à jour que les distances des nodes qui n'ont pas encore été visités.
3. Répéter l'étape 2 jusqu'à ce que tous les nodes soient visités.

dist(d) = min(1+3, ∞) = 4, dist(e) = min(1+4, ∞) = 5, dist(g) = min(1+2, ∞) = 3

dist(d) = min(2+4, 4) = 4

dist(f) = min(3+5, ∞) = 8

Aucun voisin ne peut être relaxé

dist(f) = min(5+8, 8) = 8

Aucun voisin ne peut être relaxé
L'algorithme se termine ici car tous les nodes sont visités
Considérations
- L'algorithme de Dijkstra n'est applicable qu'aux graph avec des poids d'edge non négatifs. Si des poids négatifs sont présents, l'algorithme de Dijkstra pourrait produire des résultats erronés. Dans ce cas, un algorithme différent comme le SPFA devrait être utilisé.
- Si plusieurs plus courts chemins existent entre deux nodes, tous seront trouvés.
- Dans les graph déconnectés, l'algorithme ne renvoie que les plus courts chemins du node source à tous les nodes appartenant à la même composante connectée que le node source.
Syntaxe
- Commande :
algo(sssp) - Paramètres :
Nom |
Type |
Spéc |
Par défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| ids / uuids | _id / _uuid |
/ | / | Non | ID/UUID du node source unique |
| direction | string | in, out |
/ | Oui | Direction du plus court chemin, ignorer la direction de l'edge si non définie |
| edge_schema_property | []@schema?.property |
Type numérique, doit LTE | / | Oui | Une ou plusieurs propriétés d'edge à utiliser comme poids d'edge, où les valeurs de plusieurs propriétés sont additionnées; traiter le graph comme non pondéré si non défini |
| record_path | int | 0, 1 |
0 |
Oui | 1 pour retourner les plus courts chemins, 0 pour retourner les distances les plus courtes |
| sssp_type | string | dijkstra |
dijkstra |
Oui | Pour exécuter l'algorithme SSSP de Dijkstra, gardez-le comme dijkstra |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
| order | string | asc, desc |
/ | Oui | Trier les nodes par la distance la plus courte depuis le node source |
Exemples
Le graph exemple est le suivant :
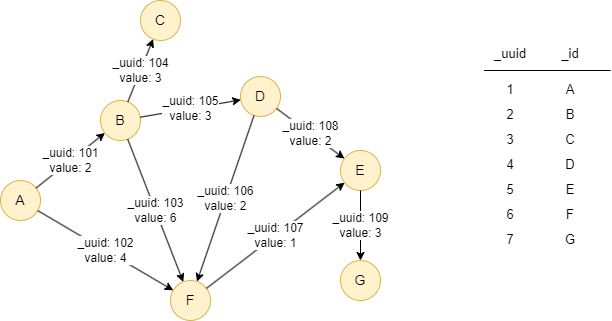
File Writeback
| Spéc | record_path |
Contenu | Description |
|---|---|---|---|
| filename | 0 | _id,totalCost |
La distance/coût le plus court du node source à chaque autre node |
| 1 | _id--_uuid--_id |
Le plus court chemin du node source à chaque autre node, le chemin est représenté par l'ID alternant des nodes et l'UUID des edges qui forment le chemin |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value'
}).write({
file: {
filename: 'costs'
}
})
Résultats : Fichier costs
G,8
F,4
E,5
D,5
C,5
B,2
A,0
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'dijkstra',
record_path: 1
}).write({
file: {
filename: 'paths'
}
})
Résultats : Fichier paths
A--[102]--F--[107]--E--[109]--G
A--[102]--F--[107]--E
A--[101]--B--[105]--D
A--[101]--B--[104]--C
A--[102]--F
A--[101]--B
A
Direct Return
| Alias Ordinal | record_path |
Type | Description | Colonnes |
|---|---|---|---|---|
| 0 | 0 | []perNode | Le coût/la distance le plus court du node source à chaque autre node | _uuid, totalCost |
| 1 | []perPath | Le plus court chemin du node source à chaque autre node, le chemin est représenté par l'UUID alternant des nodes et l'UUID des edges qui forment le chemin | / |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'dijkstra',
record_path: 0,
order: 'desc'
}) as costs
return costs
Résultats : costs
| _uuid | totalCost |
|---|---|
| 7 | 8 |
| 5 | 5 |
| 4 | 5 |
| 3 | 5 |
| 6 | 4 |
| 2 | 2 |
| 1 | 0 |
algo(sssp).params({
ids: 'A',
edge_schema_property: '@default.value',
direction: 'out',
record_path: 1,
order: 'asc'
}) as paths
return paths
Résultats : paths
| 1 |
| 1--[101]--2 |
| 1--[102]--6 |
| 1--[102]--6--[107]--5 |
| 1--[101]--2--[105]--4 |
| 1--[101]--2--[104]--3 |
| 1--[102]--6--[107]--5--[109]--7 |
Stream Return
| Alias Ordinal | record_path |
Type | Description | Colonnes |
|---|---|---|---|---|
| 0 | 0 | []perNode | Le coût/la distance le plus court du node source à chaque autre node | _uuid, totalCost |
| 1 | []perPath | Le plus court chemin du node source à chaque autre node, le chemin est représenté par l'UUID alternant des nodes et l'UUID des edges qui forment le chemin | / |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'dijkstra'
}).stream() as costs
where costs.totalCost <> [0,5]
return costs
Résultats : costs
| _uuid | totalCost |
|---|---|
| 6 | 4 |
| 2 | 2 |
algo(sssp).params({
ids: 'A',
edge_schema_property: '@default.value',
record_path: 1
}).stream() as p
where length(p) <> [0,3]
return p
Résultats : p
| 1--[102]--6--[107]--5 |
| 1--[101]--2--[105]--4 |
| 1--[101]--2--[104]--3 |
| 1--[102]--6 |
| 1--[101]--2 |

