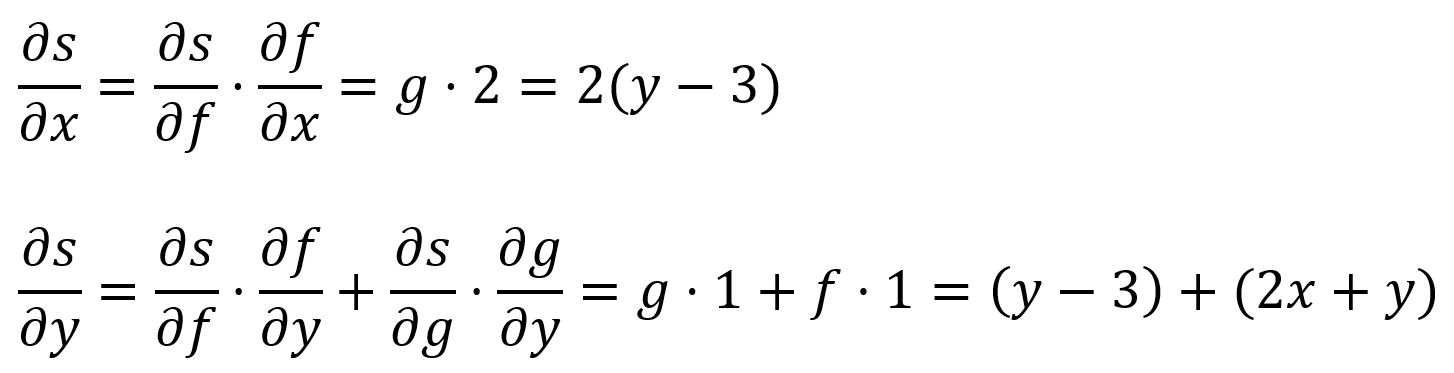Le gradient descent est un algorithme d'optimisation fondamental largement utilisé dans les embeddings de graphes. Son objectif principal est d'ajuster de manière itérative les paramètres d'un modèle d'embedding de graphe pour minimiser une fonction de perte/coût prédéfinie.
Plusieurs variations du gradient descent ont émergé, chacune conçue pour traiter des défis spécifiques associés aux tâches d'embedding de graphes à grande échelle. Des variations notables incluent le Gradient Descent Stochastique (SGD) et le Mini-Batch Gradient Descent (MBGD). Ces variations mettent à jour les paramètres du modèle en utilisant le gradient calculé à partir d'un seul ou d'un plus petit sous-ensemble de données lors de chaque itération.
Forme de Base
Considérons un scénario réel : imaginez-vous debout au sommet d'une montagne et voulant descendre le plus vite possible. Naturellement, il existe un chemin optimal vers le bas, mais identifier ce chemin précis est souvent une tâche ardue. Plus fréquemment, une approche pas à pas est adoptée. Essentiellement, à chaque pas vers une nouvelle position, la prochaine action est déterminée en calculant la direction (c'est-à-dire, le gradient descent) qui permet la descente la plus raide, permettant ainsi le mouvement vers le point suivant dans cette direction. Ce processus itératif persiste jusqu'à atteindre le pied de la montagne.
Revolvant autour de ce concept, le gradient descent sert de technique pour identifier la valeur minimale le long de la descente du gradient. Inversement, si l'objectif est de localiser la valeur maximale tout en montant le long de la direction du gradient, l'approche devient un gradient ascent.
Étant donné une fonction , la forme de base du gradient descent est :
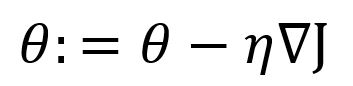
où est le gradient de la fonction à la position de , est le taux d'apprentissage. Puisque le gradient est la direction de la montée la plus raide, un symbole négatif est utilisé avant pour obtenir la descente la plus raide.
Le taux d'apprentissage détermine la longueur de chaque pas le long de la direction du gradient descent vers la cible. Dans l'exemple ci-dessus, le taux d'apprentissage peut être considéré comme la distance parcourue à chaque pas effectué.
Le taux d'apprentissage reste généralement constant pendant le processus d'entraînement du modèle. Cependant, des variations et des adaptations du modèle pourraient incorporer un calendrier de taux d'apprentissage, où le taux d'apprentissage pourrait être ajusté au cours de l'entraînement, diminuant progressivement ou selon des calendriers prédéfinis. Ces ajustements sont conçus pour améliorer la convergence et l'efficacité de l'optimisation.
Exemple : Fonction à Variable Unique
Pour la fonction , son gradient (dans ce cas, identique à la dérivée) est .
Si on commence à la position , et qu'on règle , les mouvements suivants selon le gradient descent seraient :
- ...
- ...
Au fur et à mesure que le nombre de pas augmente, nous convergerons progressivement vers la position , atteignant finalement la valeur minimale de la fonction.
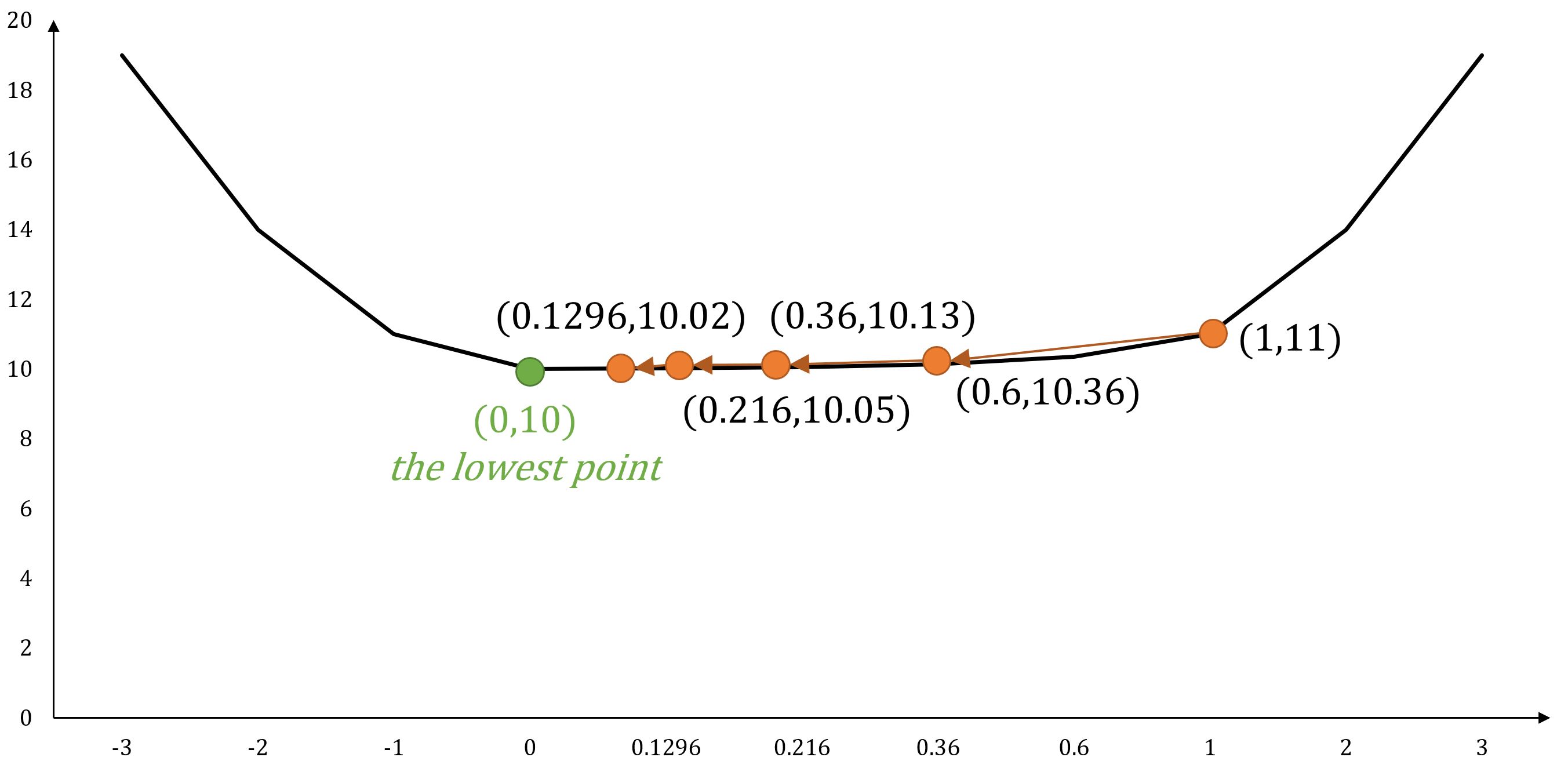
Exemple : Fonction à Variables Multiples
Pour la fonction , son gradient est .
Si on commence à la position , et qu'on règle , les mouvements suivants selon le gradient descent seraient :
- ...
- ...
Au fur et à mesure que le nombre de pas augmente, nous convergerons progressivement vers la position , atteignant finalement la valeur minimale de la fonction.
Application dans les Embeddings de Graphe
Dans le processus d'entraînement d'un modèle de réseau de neurones dans les embeddings de graphe, une fonction de perte ou de coût, notée , est fréquemment utilisée pour évaluer la disparité entre la sortie du modèle et le résultat attendu. La technique du gradient descent est ensuite appliquée pour minimiser cette fonction de perte. Cela implique d'ajuster de manière itérative les paramètres du modèle dans la direction opposée au gradient jusqu'à convergence, optimisant ainsi le modèle.
Pour trouver un équilibre entre l'efficacité computationnelle et l'exactitude, plusieurs variantes du gradient descent ont été employées dans la pratique, y compris :
- Gradient Descent Stochastique (SGD)
- Mini-Batch Gradient Descent (MBGD)
Exemple
Considérons un scénario où nous utilisons un ensemble de échantillons pour entraîner un modèle de réseau de neurones. Chaque échantillon se compose de valeurs d'entrée et de leurs sorties attendues correspondantes. Utilisons et () pour désigner la ème valeur d'entrée et la sortie attendue.
L'hypothèse du modèle est définie comme :
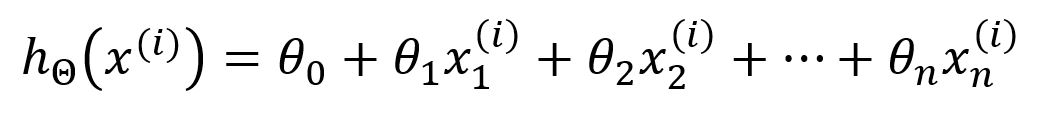
Ici, représente les paramètres du modèle ~ , et est le vecteur d'entrée -ème, constitué de caractéristiques. Le modèle utilise la fonction pour calculer la sortie en effectuant une combinaison pondérée des caractéristiques d'entrée.
L'objectif de l'entraînement du modèle est d'identifier les valeurs optimales de qui conduisent à ce que les sorties soient aussi proches que possible des valeurs attendues. Au début de l'entraînement, se voit attribuer des valeurs aléatoires.
Lors de chaque itération d'entraînement du modèle, une fois que les sorties pour tous les échantillons ont été calculées, l'erreur quadratique moyenne (MSE) est utilisée comme fonction de perte/coût pour mesurer l'erreur moyenne entre chaque sortie calculée et sa valeur attendue correspondante :
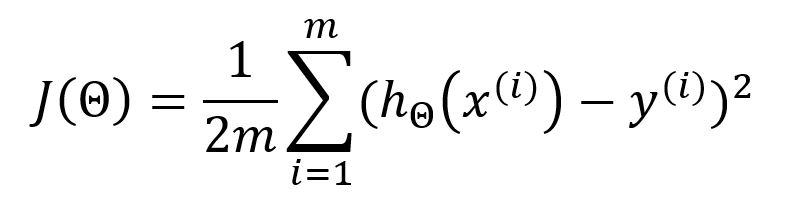
Dans la formule standard du MSE, le dénominateur est généralement . Cependant, est souvent utilisé à la place pour compenser le terme au carré lorsque la fonction de perte est dérivée, ce qui conduit à l'élimination du coefficient constant dans le but de simplifier les calculs ultérieurs. Cette modification n'affecte pas les résultats finaux.
Subséquemment, le gradient descent est employé pour mettre à jour les paramètres . La dérivée partielle par rapport à est calculée comme suit :
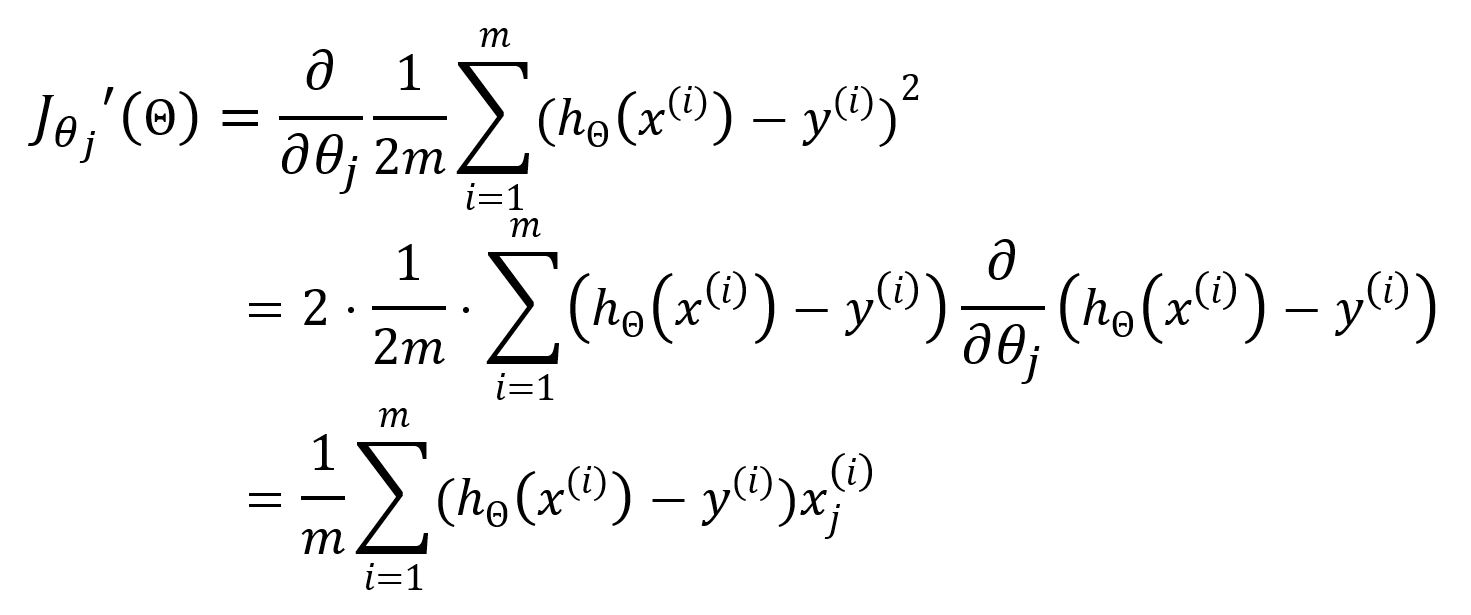
Ainsi, mettez à jour comme:
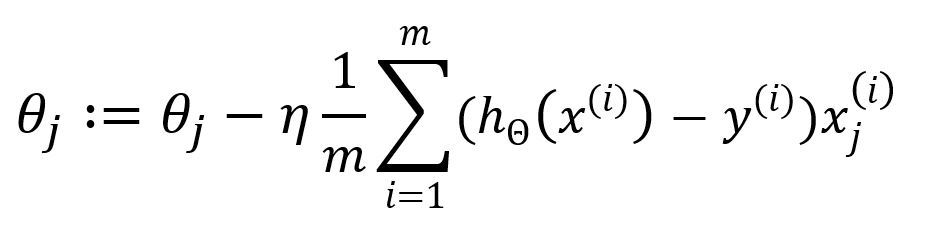
La sommation de à indique que tous les échantillons sont utilisés à chaque itération pour mettre à jour les paramètres. Cette approche est connue sous le nom de Batch Gradient Descent (BGD), qui est la forme originale et la plus simple de l'optimisation par gradient descent. Dans le BGD, l'ensemble du jeu de données d'échantillons est utilisé pour calculer le gradient de la fonction de coût à chaque itération.
Bien que le BGD puisse garantir une convergence précise vers le minimum de la fonction de coût, il peut être intensif en calcul pour de grands ensembles de données. Comme solution, le SGD et le MBGD ont été développés pour traiter l'efficacité et la vitesse de convergence. Ces variations utilisent des sous-ensembles de données à chaque itération, rendant le processus d'optimisation plus rapide tout en cherchant à trouver les paramètres optimaux.
Gradient Descent Stochastique
Le gradient descent stochastique (SGD) sélectionne aléatoirement un seul échantillon pour calculer le gradient à chaque itération.
Lors de l'utilisation du SGD, la fonction de perte ci-dessus doit être exprimée comme suit :
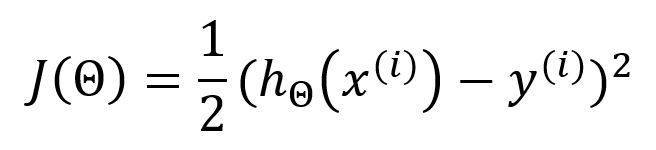
La dérivée partielle par rapport à est :
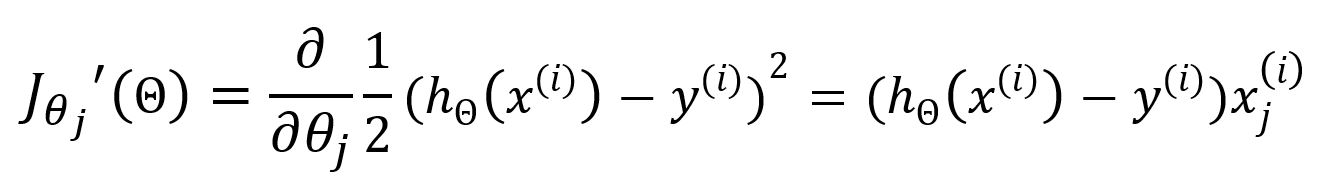
Mettez à jour comme :
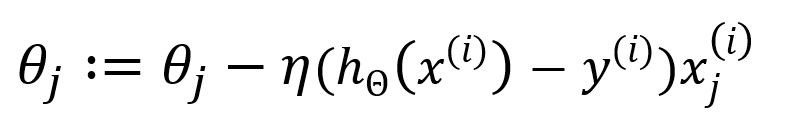
La complexité computationnelle est réduite dans le SGD puisqu'il n'utilise qu'un seul échantillon, contournant ainsi la nécessité de sommation et d'averaging. Bien que cela améliore la vitesse de calcul, cela se fait au détriment d'un certain degré de précision.
Mini-Batch Gradient Descent
Le BGD et le SGD représentent tous deux des extrêmes - l'un impliquant tous les échantillons et l'autre un seul échantillon. Le Mini-Batch Gradient Descent (MBGD) trouve un équilibre en sélectionnant de manière aléatoire un sous-ensemble de échantillons pour le calcul.
Bases Mathématiques
Dérivée
La dérivée d'une fonction à une seule variable est souvent notée ou , elle représente comment change par rapport à un léger changement de à un point donné.
Graphiquement, correspond à la pente de la ligne tangente à la courbe de la fonction. La dérivée au point est :
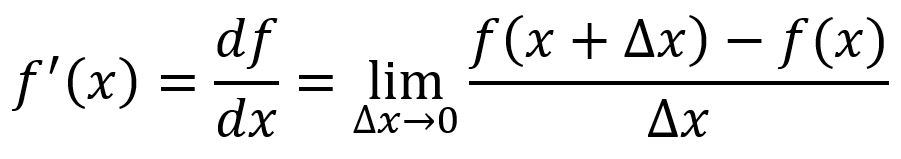
Par exemple, , au point :
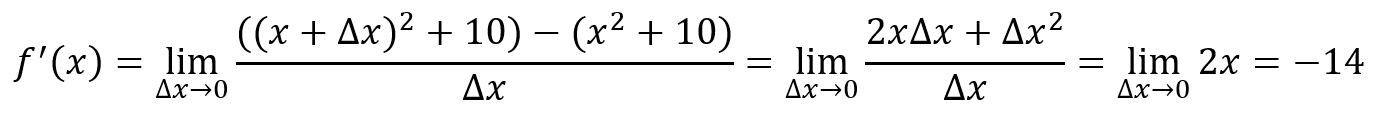
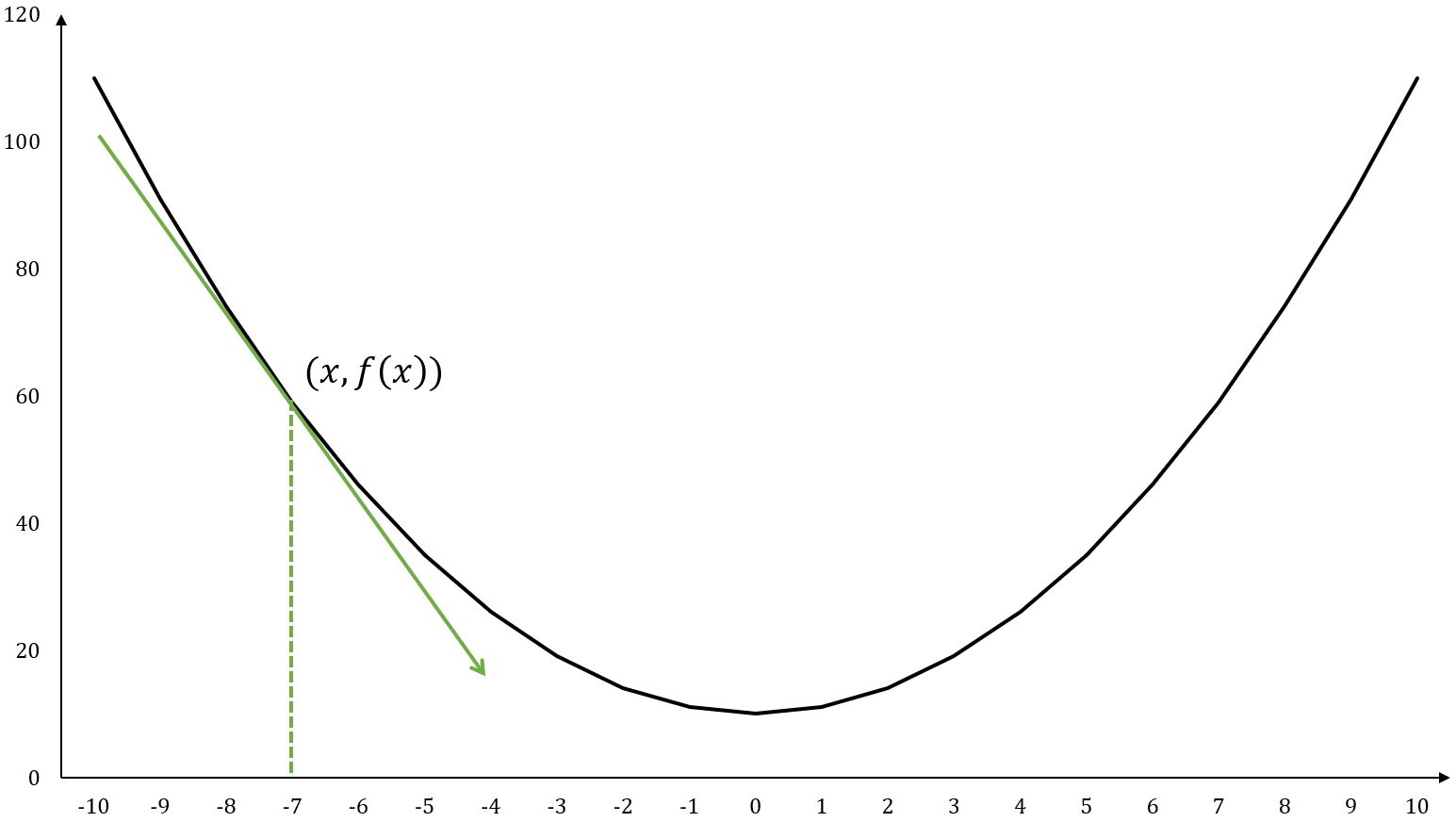
La ligne tangente est une ligne droite qui touche simplement la courbe de la fonction en un point spécifique et partage la même direction que la courbe à ce point.
Dérivée Partielle
La dérivée partielle d'une fonction à plusieurs variables mesure comment la fonction change lorsque l'on fait varier une variable spécifique tout en gardant constantes toutes les autres variables. Pour une fonction , sa dérivée partielle par rapport à en un point particulier est notée ou :
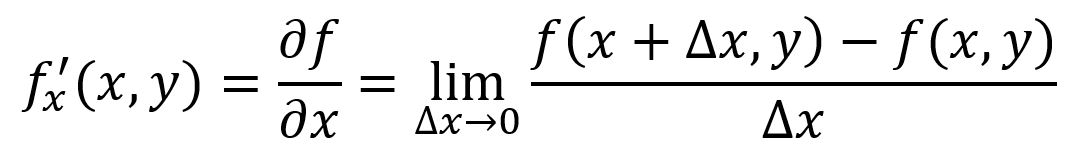
Par exemple, , au point , :
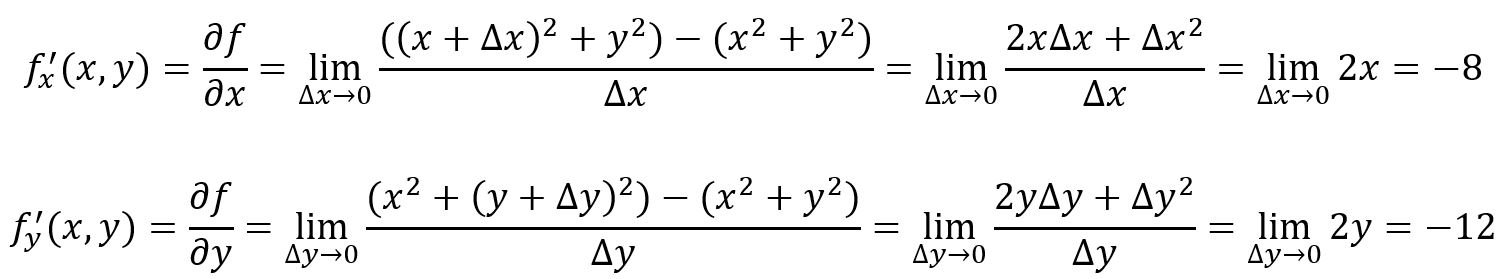
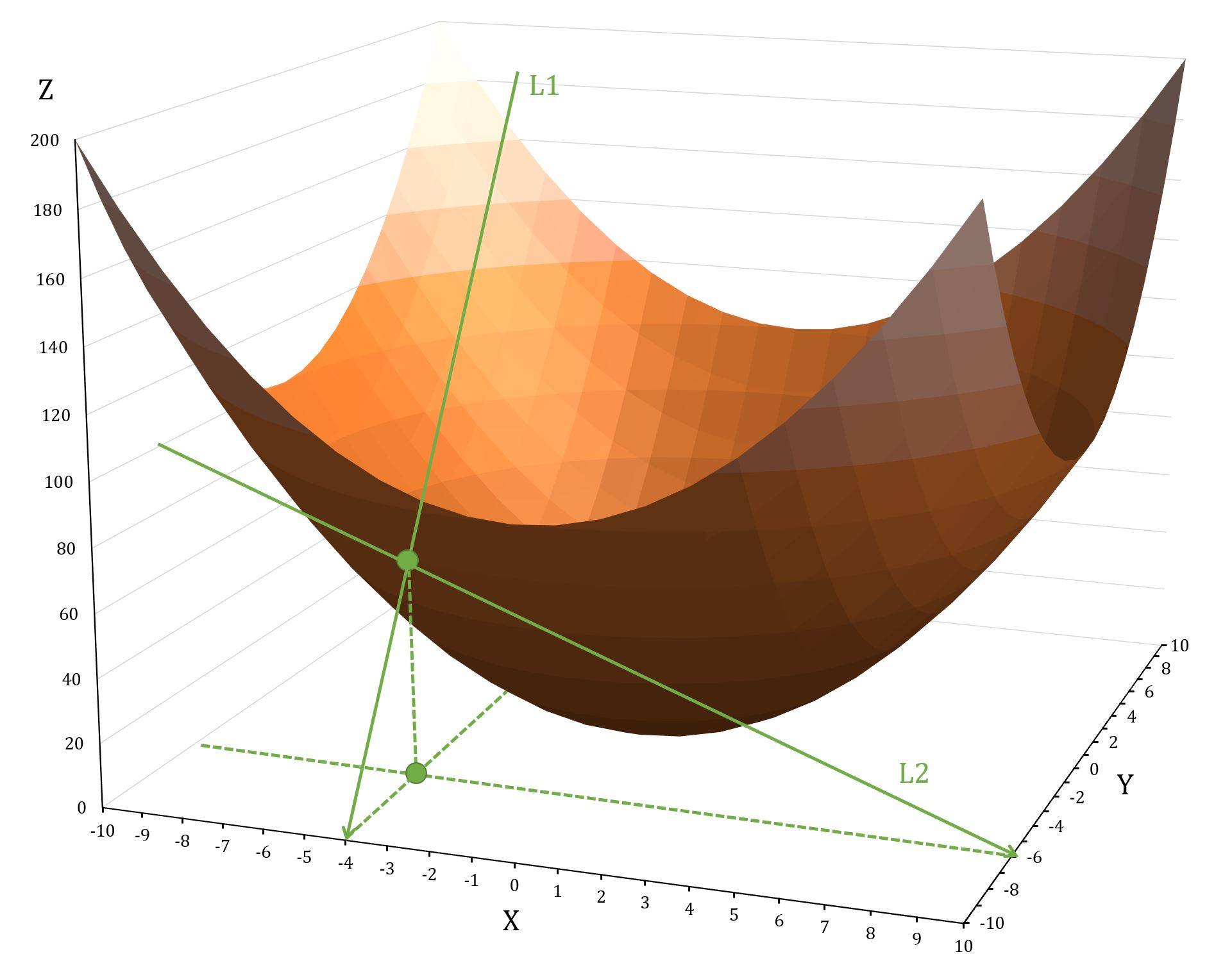
montre comment la fonction change lorsque vous vous déplacez le long de l'axe des Y, tout en gardant constant; montre comment la fonction change lorsque vous vous déplacez le long de l'axe des X, tout en gardant constant.
Dérivée Directionnelle
La dérivée partielle d'une fonction indique les changements de la sortie lorsque l'on se déplace légèrement dans les directions des axes. Mais lorsque nous nous déplaçons dans une direction qui n'est pas parallèle à l'un des axes, le concept de dérivée directionnelle devient crucial.
La dérivée directionnelle est mathématiquement exprimée comme le produit scalaire du vecteur composé de toutes les dérivées partielles de la fonction avec le vecteur unitaire qui indique la direction du changement :
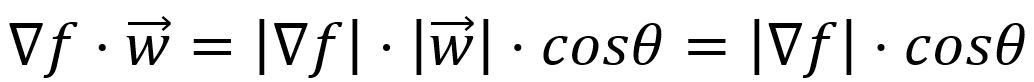
où , est l'angle entre les deux vecteurs, et
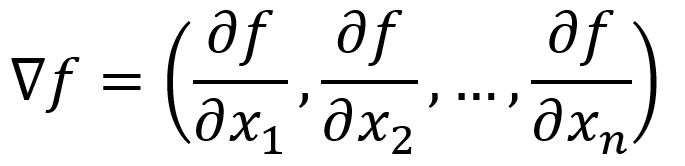
Gradient
Le gradient est la direction où la sortie d'une fonction a la montée la plus raide. Cela équivaut à trouver la maximale dérivée directionnelle. Cela se produit lorsque l'angle entre les vecteurs et est de , car , impliquant que s'aligne avec la direction de . est ainsi appelé le gradient d'une fonction.
Naturellement, le gradient négatif pointe dans la direction de la descente la plus raide.
Règle de la Chaîne
La règle de la chaîne décrit comment calculer la dérivée d'une fonction composite. Sous sa forme la plus simple, la dérivée d'une fonction composite peut être calculée en multipliant la dérivée de par rapport à par la dérivée de par rapport à :
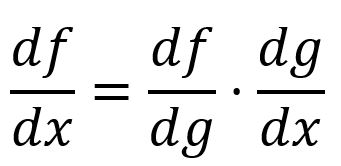
Par exemple, est composé de et :
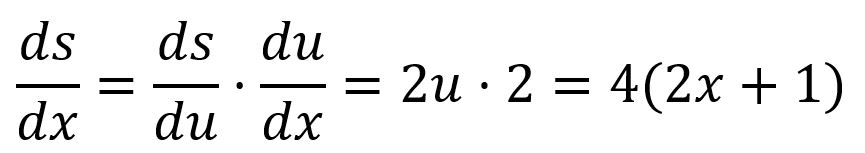
Dans une fonction composite à plusieurs variables, les dérivées partielles sont obtenues en appliquant la règle de la chaîne à chaque variable.
Par exemple, est composé de et et :