Vue d’ensemble

L'algorithme des k-Edge Connected Components vise à trouver des groupes de nodes ayant des interconnexions solides basées sur leurs edges. En considérant la connectivité des edges plutôt que seulement les nodes eux-mêmes, l'algorithme peut révéler des clusters ou des communautés au sein du graph où les nodes sont fortement liés entre eux. Cette information peut être précieuse pour diverses applications, notamment l'analyse des réseaux sociaux, l'analyse des web graphs, l'analyse des réseaux biologiques, etc.

Matériel relatif à l'algorithme:

• T. Wang, Y. Zhang, F.Y.L. Chin, H. Ting, Y.H. Tsin, S. Poon, A Simple Algorithm for Finding All k-Edge-Connected Components (2015)

Concepts

Connectivité d'Edge

La connectivité d'Edge d'un graph est une mesure qui quantifie le nombre minimum d'edges qu'il faut retirer pour déconnecter le graph ou réduire sa connectivité. Elle représente la résilience d'un graph face aux défaillances des edges. Étant donné un graph G = (V, E), G est k-arêtes connecté s'il reste connecté après le retrait de n'importe quel k-1 ou moins edges de G.

La connectivité d'Edge peut également être interprétée comme le nombre maximum de paths disjoints d'arêtes entre n'importe quels deux nodes dans le graph. Si la connectivité d'Edge d'un graph est k, cela signifie qu'il y a k paths disjoints d'arêtes entre chaque paire de nodes dans le graph.

Ci-dessous montre un graph 3-arêtes connecté et les paths disjoints d'arêtes entre chaque paire de nodes.

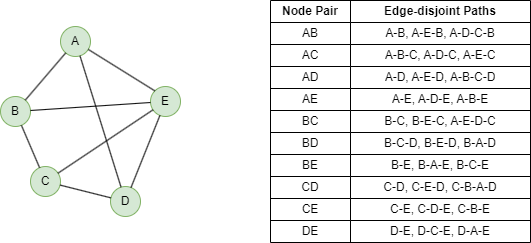
Les paths disjoints d'arêtes sont des paths qui n'ont aucun edge en commun.

k-Edge Connected Components

Au lieu de déterminer si l'ensemble du graph G est k-arêtes connecté, l'algorithme des k-Edge Connected Components cherche à trouver les sous-ensembles maximaux de nodes V_i ⊆ V, où les sous-graphs induits par V_i sont k-arêtes connectés.

Par exemple, dans les réseaux sociaux, trouver un groupe de personnes fortement connectées est plus important que de calculer la connectivité de l'ensemble du réseau social.

Considérations

• Pour k = 1, ce problème est équivalent à trouver les composants connectés de G.
• L'algorithme des k-Edge Connected Components ignore la direction des edges mais les calcule comme des edges non orientés.

Syntaxe

• Commande: algo(kcc)
• Paramètres:

Exemples

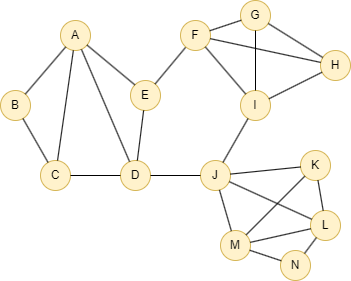
Le graph d'exemple est le suivant:

File Writeback

algo(kcc).params({
  k: 3
}).write({
  file:{
    filename: 'result'
  }
})

Résultats: Fichier result

F,G,I,H,
J,K,M,L,