Vue d’ensemble
L'algorithme de k-Truss identifie le sous-graphe cohésif maximal appelé truss dans le graph. Il a des applications étendues dans divers domaines, y compris les réseaux sociaux, les réseaux biologiques et les réseaux de transport. En découvrant des communautés ou des clusters de nodes étroitement liés, l'algorithme de k-Truss fournit des informations précieuses sur la structure et la connectivité des réseaux complexes.
Les k-Truss ont été initialement définis par J. Cohen en 2005 :
- J. Cohen, Trusses: Cohesive Subgraphs for Social Network Analysis (2005)
Concepts
k-Truss
Le truss est motivé par une observation naturelle de la cohésion sociale: si deux personnes sont fortement liées, il est probable qu'elles partagent également des liens avec d'autres. Le k-Truss est ainsi créé de cette manière : un lien entre A et B est considéré légitime seulement s'il est soutenu par au moins k–2 autres personnes qui sont chacune liées à A et à B. En d'autres termes, chaque edge dans un k-truss relie deux nodes qui ont au moins k–2 voisins communs.
La définition formelle est qu'un k-truss est un sous-graphe maximal dans le graph tel que chaque edge est soutenu par au moins k–2 paires d'edges formant des triangles avec cet edge.
L'ensemble du graph est montré ci-dessous, le 3-truss et le 4-truss sont soulignés en rouge. Ce graph n'a pas de truss avec une valeur de k de 5 ou plus.
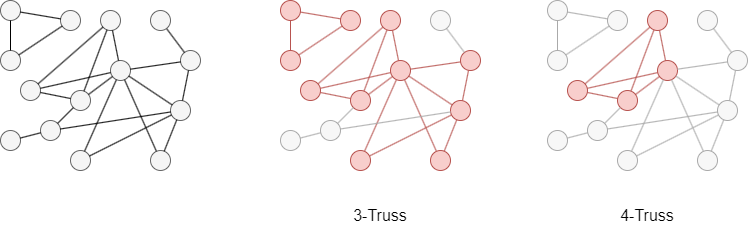
L'algorithme de k-Truss d'Ultipa identifie le truss maximal dans chaque composante connectée.
Considérations
- Au moins 3 nodes sont contenus dans un truss (lorsque k≥3).
- Dans un graph complexe où plusieurs edges peuvent exister entre deux nodes, les triangles dans un truss sont comptés par edges. Veuillez également vous référer à l'algorithme Triangle Counting.
- L'algorithme de k-Truss ignore la direction des edges mais les calcule comme des edges non dirigés.
Syntaxe
- Commande :
algo(k_truss) - Paramètres :
Nom |
Type |
Spec |
Par défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| k | int | ≥2 | / | No | Chaque edge dans le k-truss est contenu dans au moins k − 2 triangles |
Exemples
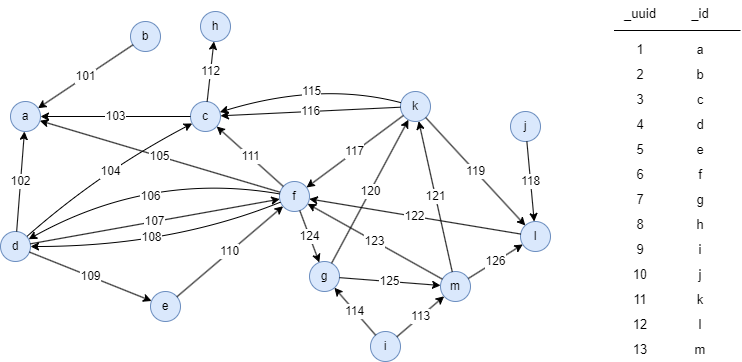
Le graph d'exemple est le suivant :
File Writeback
Spec |
Contenu |
Description |
|---|---|---|
| filename | _id--[_uuid]--_id |
Chemin à un pas dans le truss: (start node)--(edge)--(end node) |
algo(k_truss).params({k: 4}).write({
file:{
filename: 'truss'
}
})
Résultats : Fichier truss
d--[102]--a
c--[103]--a
d--[104]--c
f--[105]--a
f--[106]--d
d--[107]--f
f--[108]--d
d--[109]--e
e--[110]--f
f--[111]--c
k--[117]--f
k--[119]--l
g--[120]--k
m--[121]--k
i--[122]--f
m--[123]--f
f--[124]--g
g--[125]--m
m--[126]--l
Direct Return
Alias Ordinal |
Type |
Description |
|---|---|---|
| 0 | []path |
Chemin à un pas dans le truss: _uuid (start node) -- [_uuid] (edge) -- _uuid (end node) |
algo(k_truss).params({k: 5}) as truss return truss
Résultats : subgraph
| 4--[102]--1 |
| 4--[104]--3 |
| 6--[105]--1 |
| 6--[106]--4 |
| 4--[107]--6 |
| 6--[108]--4 |
| 4--[109]--5 |
| 5--[110]--6 |
| 6--[111]--3 |
Stream Return
Alias Ordinal |
Type |
Description |
|---|---|---|
| 0 | []path |
Chemin à un pas dans le truss: _uuid (start node) -- _uuid (edge) -- _uuid (end node) |
algo(k_truss).params({k: 5}).stream() as truss5
with pedges(truss5) as e
find().edges(e) as edges
return edges{*}
Résultats : edges
| _uuid | _from | _to | _from_uuid | _to_uuid |
|---|---|---|---|---|
| 102 | d | a | 4 | 1 |
| 104 | d | c | 4 | 3 |
| 105 | f | a | 6 | 1 |
| 106 | f | d | 6 | 4 |
| 107 | d | f | 4 | 6 |
| 108 | f | d | 6 | 4 |
| 109 | d | e | 4 | 5 |
| 110 | e | f | 5 | 6 |
| 111 | f | c | 6 | 3 |

