Vue d’ensemble
PageRank a été initialement proposé dans le contexte du World Wide Web (WWW), il exploite la structure des liens du WWW pour produire un classement objectif global de 'l'importance' des pages web qui peut être utilisé par les moteurs de recherche. Cet algorithme a été proposé en 1997-1998 par les cofondateurs de Google Larry Page et Sergey Brin.
- L. Page, S Brin, R. Motwani, T. Winograd, The PageRank Citation Ranking: Bringing Order to The Web (1998)
Avec le développement de la technologie et l'émergence de vastes données de corrélation, PageRank a été adopté dans de nombreux autres domaines également.
Concepts
Structure des Liens et PageRank
Dans le WWW, les hypertextes contenus dans les pages web créent des liens entre les pages web. Chaque page web (node) peut avoir des liens sortants (via out-edges) et des liens entrants (via in-edges). Dans le graphique suivant, A et B sont des liens entrants de C, D est un lien sortant de C.
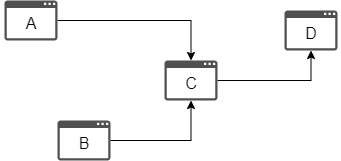
Les pages web varient considérablement en termes du nombre de liens entrants qu'elles ont. Naturellement, les pages web qui sont plus importantes, autoritaires ou de haute qualité sont susceptibles de recevoir des liens entrants plus nombreux ou plus importants.
PageRank peut être décrit ainsi : une page a un rang élevé si la somme des rangs de ses liens entrants est élevée. Cela couvre à la fois le cas où une page a de nombreux liens entrants et celui où une page a quelques liens entrants avec un rang élevé.
Propagation du Rang
Les rangs (scores) de toutes les pages sont calculés de manière récursive en commençant par un ensemble quelconque de rangs et en itérant le calcul jusqu'à ce qu'il converge. À chaque itération, une page distribue son rang à tous ses liens sortants de manière égale pour contribuer aux rangs des pages vers lesquelles elle pointe ; par ailleurs, chaque page reçoit des rangs de ses liens entrants, donc le rang de la page u après une itération est :
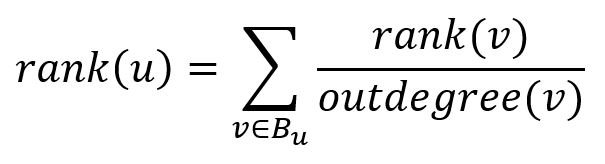
où Bu est l'ensemble des liens entrants de u.
Ci-dessous montre un état stable d'un ensemble de pages :
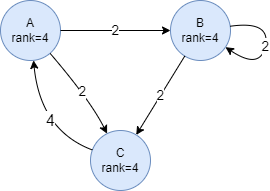
Facteur d'Amortissement
Considérons les types suivants de pages web :
- Pages web sans liens entrants. Le rang qu'elles reçoivent est 0, mais elles doivent encore être consultées sur Internet.
- Pages web sans liens sortants. Leurs rangs sont perdus du système.
- Un groupe de pages web qui ne pointent qu'à des pages à l'intérieur du groupe, mais à aucune page en dehors du groupe.
Pour surmonter ces problèmes, un facteur d'amortissement, dont la valeur est comprise entre 0 et 1, est introduit. Il donne à chaque page web un rang de base tout en affaiblissant les rangs transmis par les liens entrants. Le rang de la page u après une itération devient :
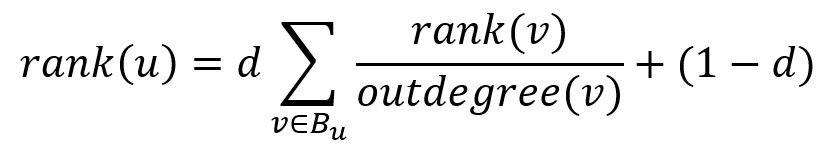
où d est le facteur d'amortissement. Par exemple, lorsque d vaut 0,7, si une page web reçoit au total 8 rangs de liens entrants, alors le rang de cette page web est mis à jour à 0,7*8 + (1-0,7) = 5,9.
Le facteur d'amortissement peut également être compris comme la probabilité qu'un internaute fasse un saut aléatoire vers une page web qui n'est pas l'un des liens sortants de la page web actuelle.
Considérations
- Le rang d'une page web isolée restera le même que la valeur de (1 - d).
- La boucle auto est considérée à la fois comme un lien sortant et un lien entrant, une page web passerait une partie de son rang à elle-même à travers la boucle auto. Si un réseau a beaucoup de boucles auto, il faudra plus d'itérations pour converger.
Syntaxe
- Commande :
algo(page_rank) - Paramètres :
Nom |
Type |
Spec |
Par défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| init_value | float | >0 | 0.2 |
Oui | Le même rang initial pour tous les nodes |
| loop_num | int | >=1 | 5 |
Oui | Nombre d'itérations |
| damping | float | (0,1) | 0.8 |
Oui | Facteur d'amortissement |
| weaken | int | 1, 2 |
1 |
Oui | Pour PageRank, gardez à 1; 2 signifie exécuter ArticleRank |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
| order | string | asc, desc |
/ | Oui | Trier les nodes par le rang |
Exemples
Le graphique d'exemple est le suivant :
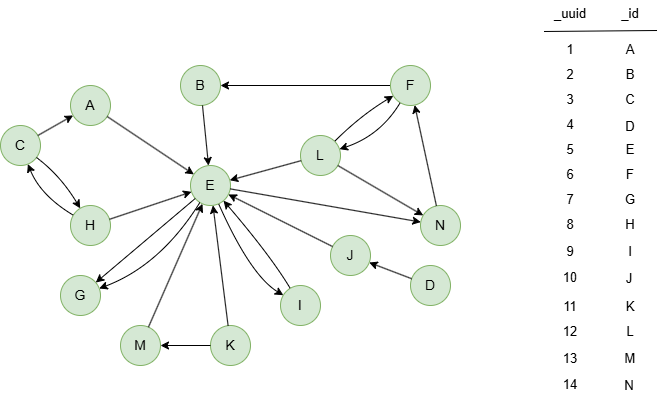
File Writeback
| Spec | Contenu |
|---|---|
| filename | _id,rank |
algo(page_rank).params({
init_value: 1,
loop_num: 50,
damping: 0.8,
weaken: 1,
order: 'desc'
}).write({
file: {filename: 'rank'}
})
Résultats : Fichier rank
E,3.96235
F,1.61052
N,1.48175
G,1.25663
I,1.25663
B,0.844209
L,0.844209
K,0.702651
M,0.48106
J,0.36
H,0.333333
A,0.333333
C,0.333333
D,0.2
Property Writeback
| Spec | Contenu | Écriture vers | Type de Données |
|---|---|---|---|
| property | rank |
Node property | float |
algo(page_rank).params({
loop_num: 50,
weaken: 1
}).write({
db:{property: 'PR'}
})
Résultats : Le rang de chaque node est écrit dans une nouvelle propriété nommée PR
Direct Return
| Ordre Alias | Type | Description | Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et son rang | _uuid, rank |
algo(page_rank).params({
init_value: 1,
loop_num: 50,
damping: 0.8,
weaken: 1,
order: 'desc',
limit: 5
}) as PR
return PR
Résultats : PR
| _uuid | rank |
|---|---|
| 5 | 3.9623489 |
| 6 | 1.6105210 |
| 14 | 1.4817491 |
| 7 | 1.2566270 |
| 9 | 1.2566270 |
Stream Return
| Ordre Alias | Type | Description | Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et son rang | _uuid, rank |
algo(page_rank).params({
loop_num: 50,
damping: 0.8,
weaken: 1,
order: 'desc',
limit: 5
}).stream() as PR
find().nodes({_uuid == PR._uuid}) as nodes
return table(nodes._id, PR.rank)
Résultats : table(nodes._id, PR.rank)
| nodes._id | PR.rank |
|---|---|
| E | 3.9623020 |
| F | 1.6104970 |
| N | 1.4817290 |
| G | 1.2566110 |
| I | 1.2566110 |

