Le modèle Skip-gram (SG) est une approche de référence conçue pour créer des embeddings de mots dans le domaine du traitement automatique du langage naturel (NLP). Il a également été utilisé dans des algorithmes d'embedding de graph tels que Node2Vec et Struc2Vec pour générer des embeddings de nodes.
Contexte
L'origine du modèle Skip-gram peut être retracée jusqu'à l'algorithme Word2Vec. Word2Vec attribue aux mots un espace vectoriel, où les mots sémantiquement similaires sont représentés par des vecteurs proches les uns des autres. Google, avec T. Mikolov et al., a introduit Word2Vec en 2013.
- T. Mikolov, K. Chen, G. Corrado, J. Dean, Efficient Estimation of Word Representations in Vector Space (2013)
- X. Rong, Word2Vec Parameter Learning Explained (2016)
Dans le domaine de l'embedding de graph, la création de DeepWalk en 2014 a marqué l'application du modèle Skip-gram pour générer des représentations vectorielles de nodes au sein de graphs. Le concept principal est de traiter les nodes comme des "mots", les séquences de nodes générées par des marches aléatoires comme des "phrases" et "corpus".
- B. Perozzi, R. Al-Rfou, S. Skiena, DeepWalk: Online Learning of Social Representations (2014)
Les méthodes d'embedding de graph suivantes, comme Node2Vec et Struc2Vec, ont amélioré l'approche DeepWalk tout en exploitant toujours le cadre du Skip-gram.
Nous illustrerons le modèle Skip-gram en utilisant le contexte de son application originale dans le traitement automatique du langage naturel.
Vue d’ensemble du Modèle
Le principe fondamental sous-jacent au Skip-gram est de prédire un ensemble de mots de contexte pour un mot cible donné. Comme illustré dans le schéma ci-dessous, le mot d'entrée, noté , est introduit dans le modèle ; celui-ci génère ensuite quatre mots de contexte liés à : , , et . Les symboles / désignent ici le contexte précédant ou suivant le mot cible. Le nombre de mots de contexte produits peut être ajusté si nécessaire.
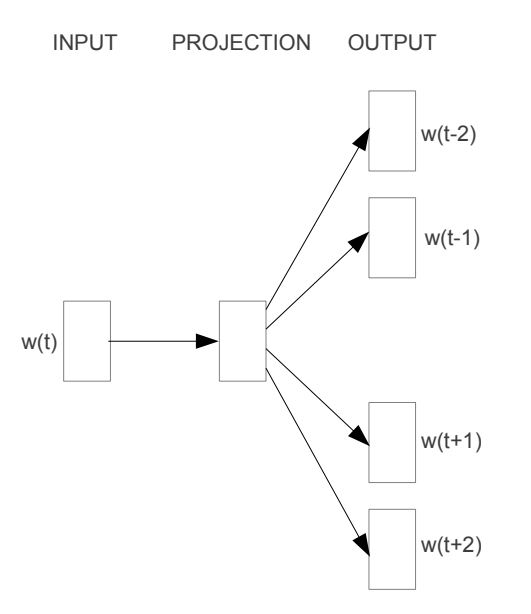
Cependant, il est important de reconnaître que l'objectif ultime du modèle Skip-gram n'est pas la prédiction. Au contraire, sa véritable tâche est de dériver la matrice de poids trouvée dans la relation de mappage (indiquée comme PROJECTION dans le schéma), qui représente efficacement les représentations vectorisées des mots.
Corpus
Un corpus est une collection de phrases ou de textes utilisés par un modèle pour apprendre les relations sémantiques entre les mots.
Considérons un vocabulaire contenant 10 mots distincts tirés d'un corpus : graph, is, a, good, way, to, visualize, data, very, at.
Ces mots peuvent être construits en phrases telles que :
Graph is a good way to visualize data.
Échantillonnage à Fenêtre Glissante
Le modèle Skip-gram utilise la technique d'échantillonnage à fenêtre glissante pour générer des échantillons d'apprentissage. Cette méthode utilise une "fenêtre" qui se déplace séquentiellement à travers chaque mot de la phrase. Le mot cible est combiné avec chaque mot de contexte avant et après lui, dans une certaine plage window_size.
Voici une illustration du processus d'échantillonnage lorsque window_size.
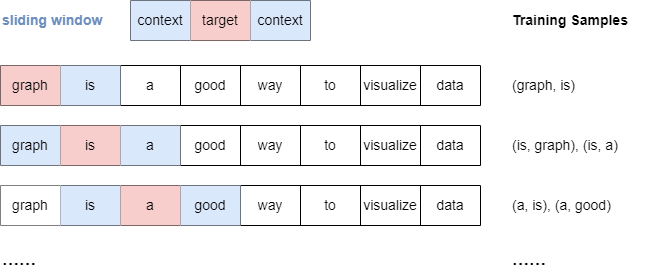
Il est important de noter que lorsque window_size, tous les mots de contexte tombant à l'intérieur de la fenêtre spécifiée sont traités également, indépendamment de leur distance par rapport au mot cible.
Encodage One-hot
Étant donné que les mots ne sont pas directement interprétables par les modèles, ils doivent être convertis en représentations compréhensibles par la machine.
Une méthode courante pour encoder les mots est l'encodage one-hot. Dans cette approche, chaque mot est représenté sous forme d'un vecteur binaire unique où un seul élément est "actif" () tandis que tous les autres sont "inactifs" (). La position du dans le vecteur correspond à l'index du mot dans le vocabulaire.
Voici comment l'encodage one-hot est appliqué à notre vocabulaire:
| Mot | Vecteur Encodé One-hot |
|---|---|
| graph | |
| is | |
| a | |
| good | |
| way | |
| to | |
| visualize | |
| data | |
| very | |
| at |
Architecture du Skip-gram
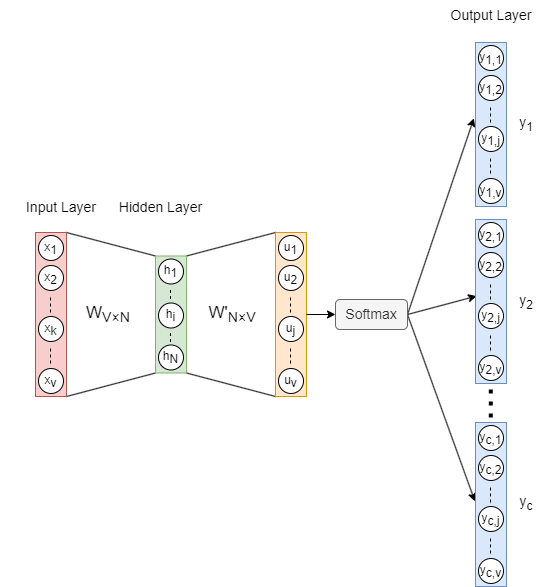
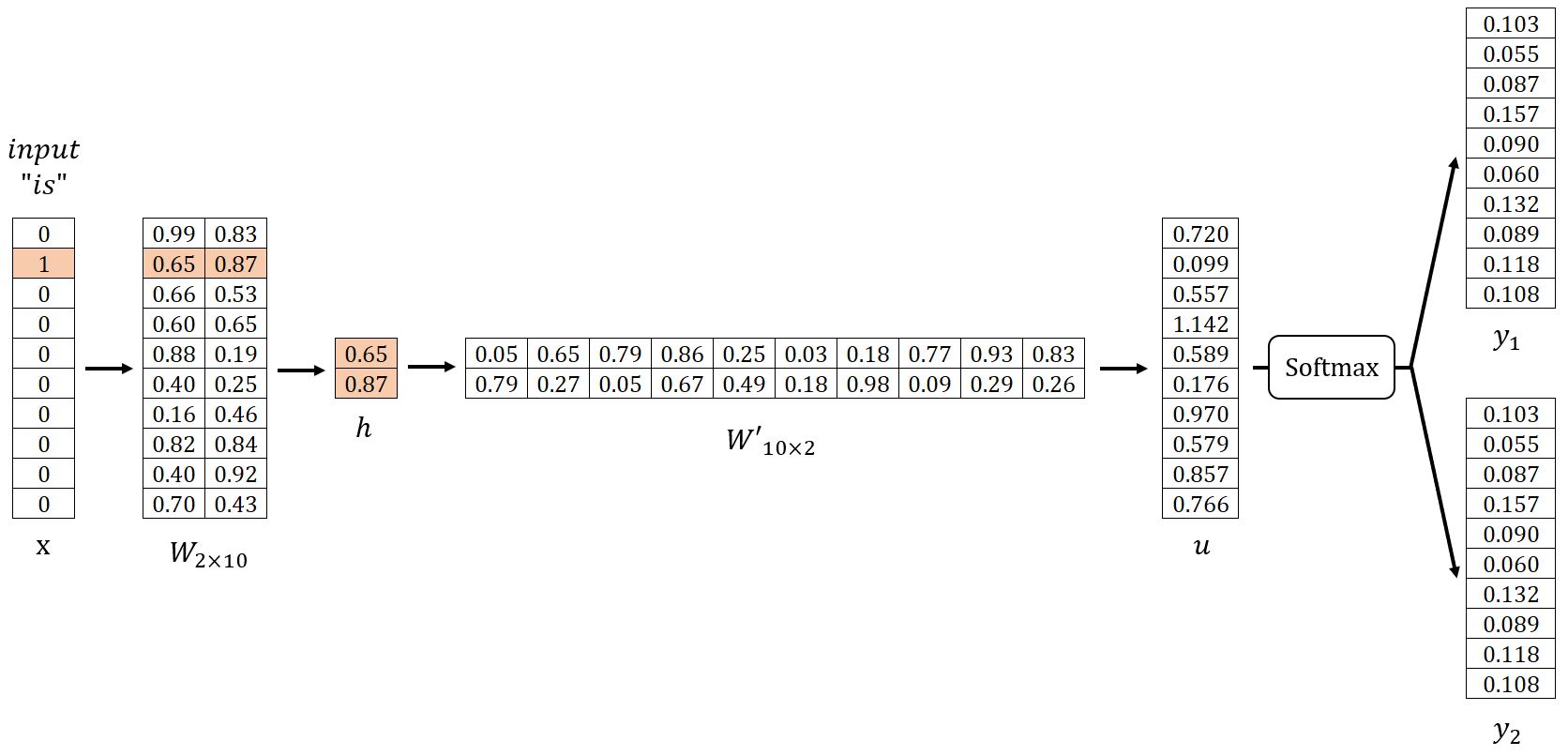
L'architecture du modèle Skip-gram est illustrée ci-dessus, où :
- Le vecteur d'entrée est l'encodage one-hot du mot cible, et est le nombre de mots dans le vocabulaire.
- est la matrice de poids entre l'entrée et le caché, et est la dimension des embeddings de mots.
- est le vecteur du layer caché.
- est la matrice de poids entre le caché et la sortie. et sont différents, n'est pas la transposition de .
- est le vecteur avant d'appliquer la fonction d'activation Softmax.
- Les vecteurs de sortie () sont également appelés panneaux, panneaux correspondant à mots de contexte du mot cible.
Softmax: La fonction Softmax joue le rôle de fonction d'activation, servant à normaliser un vecteur numérique en un vecteur de distribution de probabilité. Dans ce vecteur transformé, la somme de toutes les probabilités est égale à . La formule de la fonction Softmax est la suivante :
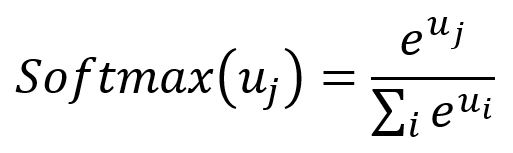
Propagation vers l'Avant
Dans notre exemple, , et fixe . Commençons par initialiser aléatoirement les matrices de poids et comme indiqué ci-dessous. Nous utiliserons ensuite l'échantillon (is, graph), (is, a) pour la démonstration.
Layer d'Entrée → Layer Caché
Obtenir le vecteur du layer caché en :
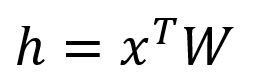
Étant donné que est un vecteur encodé one-hot avec seulement , correspond à la -ième ligne de la matrice . Cette opération est essentiellement un simple procédé de recherche :
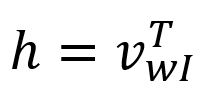
où est le vecteur d'entrée du mot cible.
En fait, chaque ligne de la matrice , notée , est considéré comme l'embedding final de chaque mot dans le vocabulaire.
Layer Caché → Layer de Sortie
Obtenir le vecteur en :
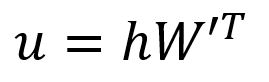
La -ième composante du vecteur est égale au produit scalaire du vecteur et la transposition du vecteur colonne -ième de la matrice :
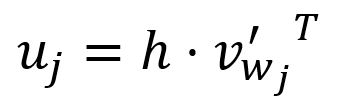
où est le vecteur de sortie du -ième mot dans le vocabulaire.
Dans la conception du modèle Skip-gram, chaque mot au sein du vocabulaire a deux représentations distinctes : le vecteur d'entrée et le vecteur de sortie . Le vecteur d'entrée sert de représentation lorsque le mot est utilisé comme cible, tandis que le vecteur de sortie représente le mot lorsqu'il agit comme contexte.
Durant le calcul, est essentiellement le produit scalaire du vecteur d'entrée du mot cible et du vecteur de sortie du -ième mot . Le modèle Skip-gram est également conçu sur le principe qu'une plus grande similarité entre deux vecteurs donne un produit scalaire plus grand de ces vecteurs.
De plus, il est important de souligner que seuls les vecteurs d'entrée sont finalement utilisés comme embeddings de mots. Cette séparation entre les vecteurs d'entrée et de sortie simplifie le processus de calcul, améliorant à la fois l'efficacité et la précision dans l'entraînement et l'inférence du modèle.
Obtenir chaque panneau de sortie en :
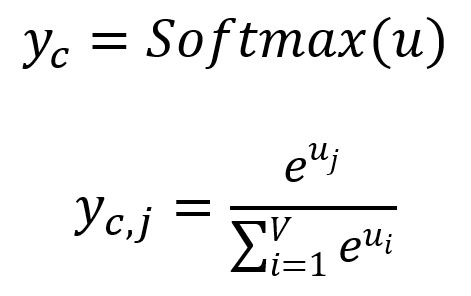
où est la -ième composante de , représentant la probabilité du -ième mot dans le vocabulaire d'être prédit tout en considérant le mot cible donné. Apparemment, la somme de toutes les probabilités est .
Les mots avec les probabilités les plus élevées sont considérés comme les mots de contexte prédits. Dans notre exemple, et les mots de contexte prédits sont good et visualize.

Rétropropagation
Pour ajuster les poids dans et , SGD est utilisé pour rétropropager les erreurs.
Fonction de Coût
Nous souhaitons maximiser les probabilités des mots de contexte , c'est-à-dire maximiser le produit de ces probabilités :
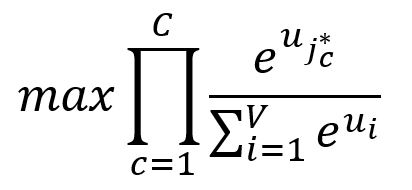
où est l'index du -ième mot de contexte de sortie attendu.
Puisque la minimisation est souvent considérée comme plus simple et pratique que la maximisation, nous effectuons quelques transformations sur l'objectif ci-dessus :
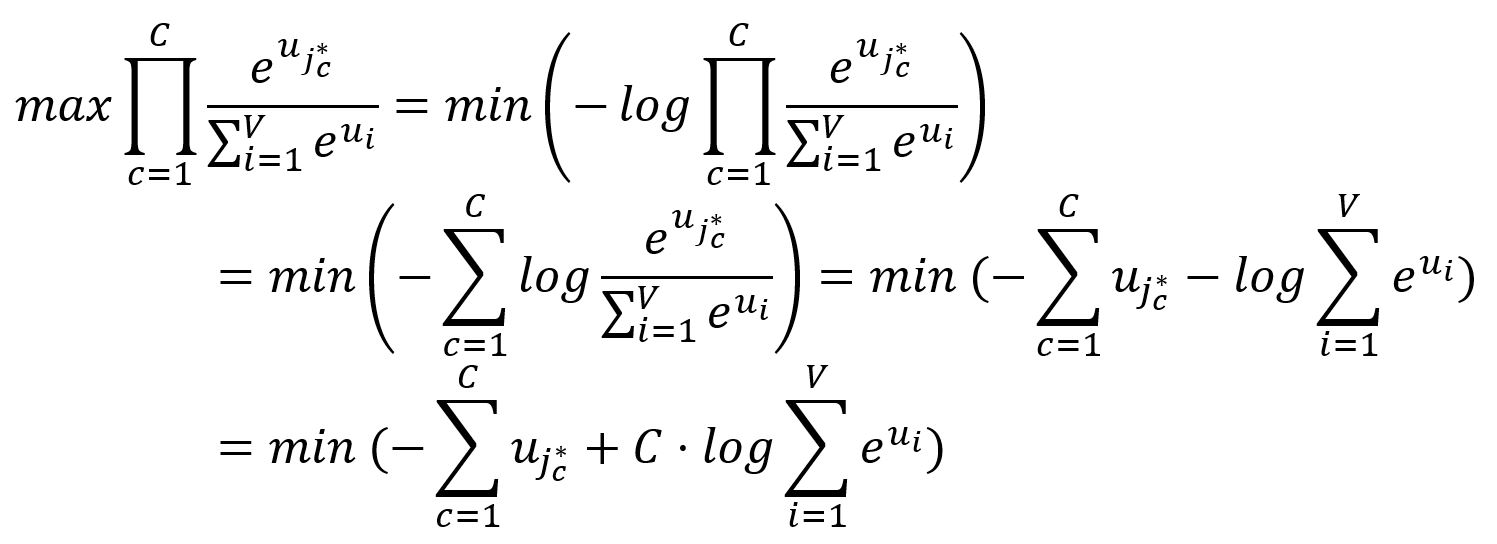
Donc, la fonction de coût du Skip-gram est exprimée comme suit :
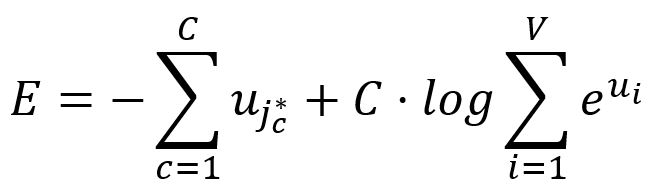
Prenez la dérivée partielle de par rapport à :
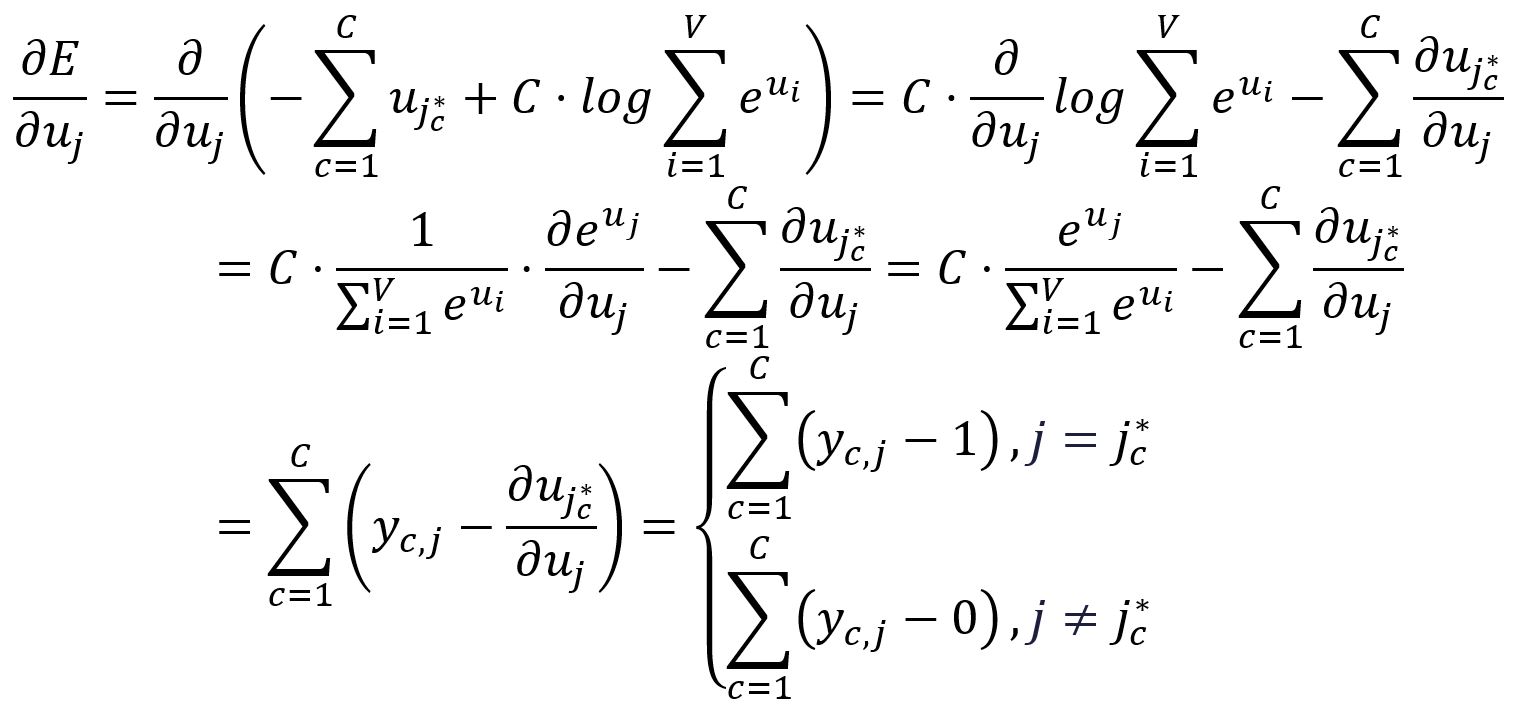
Pour simplifier la notation à l'avenir, définissez le suivant :
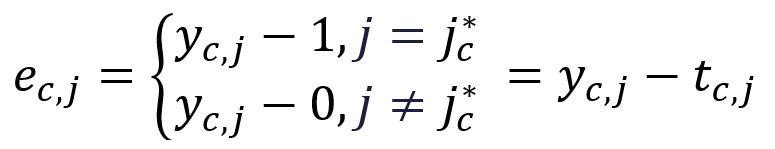
| One-hot encoding |
où est le vecteur d'encodage one-hot du -ième mot de contexte de sortie attendu. Dans notre exemple, et sont les vecteurs encodés one-hot des mots graph et a, ainsi et sont calculés comme suit :
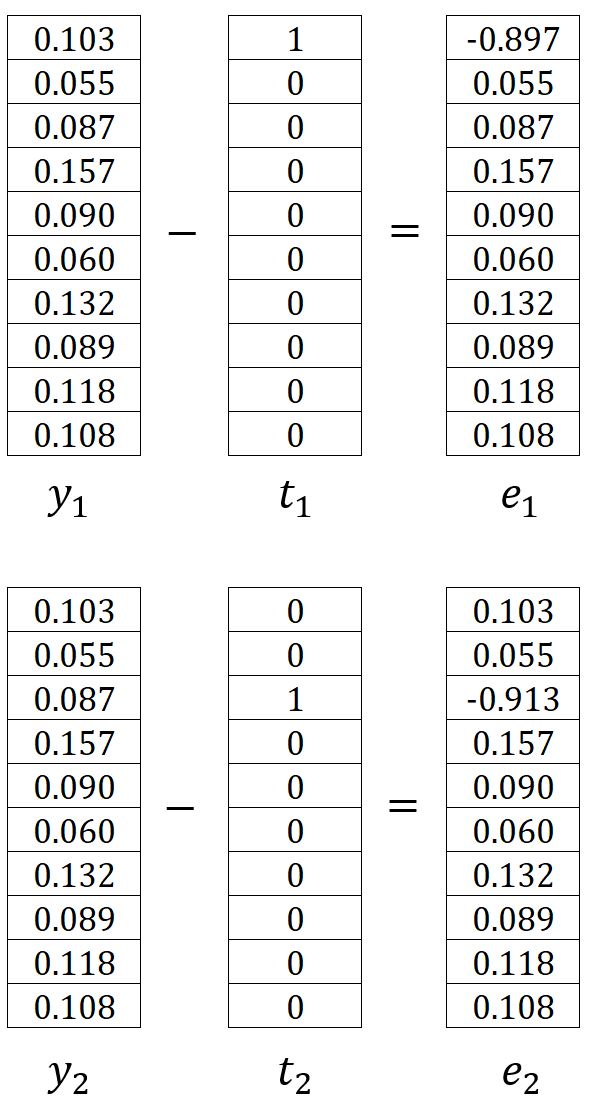
Par conséquent, peut être écrit comme suit :
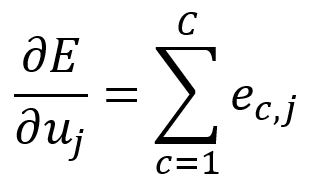
Dans notre exemple, il est calculé comme suit :
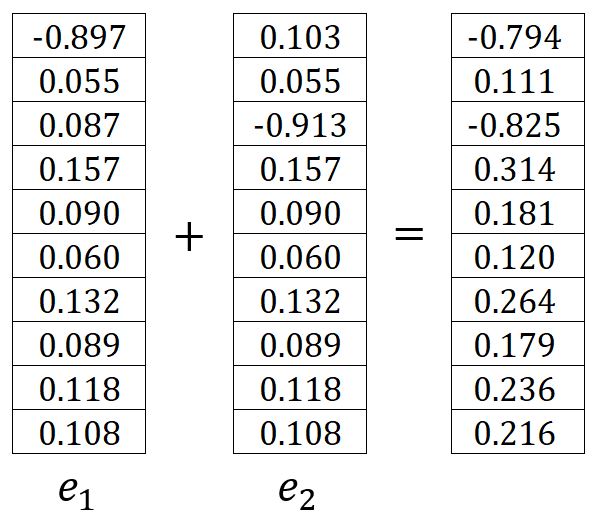
Layer de Sortie → Layer Caché
Les ajustements sont effectués pour tous les poids dans la matrice , ce qui signifie que tous les vecteurs de sortie des mots sont mis à jour.
Calculez la dérivée partielle de par rapport à :
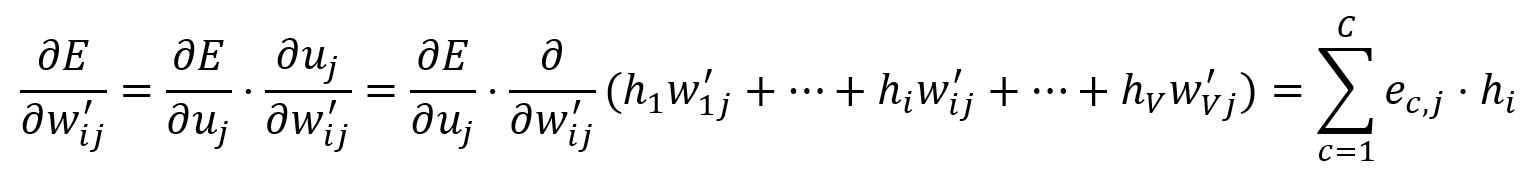
Ajustez selon le taux d'apprentissage :
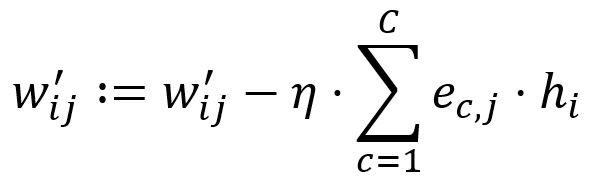
Fixez . Par exemple, et sont mis à jour en :
Layer Caché → Layer d’Entrée
Les ajustements sont effectués uniquement aux poids dans la matrice qui correspondent au vecteur d'entrée du mot cible.
Le vecteur est obtenu en ne recherchant que la -ième ligne de la matrice (étant donné que ):
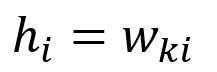
Calculez la dérivée partielle de par rapport à :
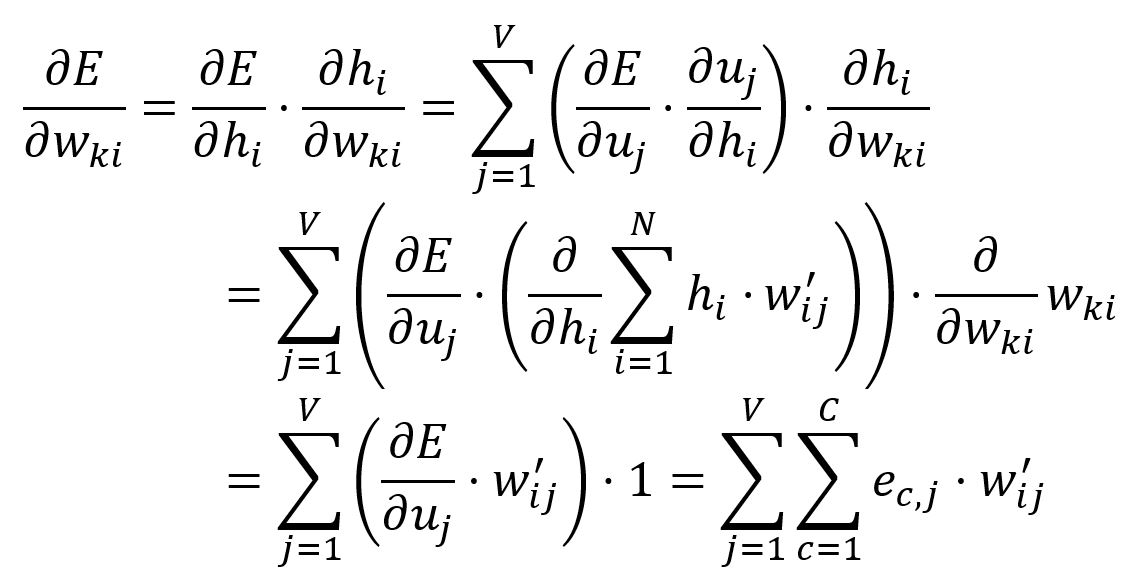
Ajustez selon le taux d'apprentissage :
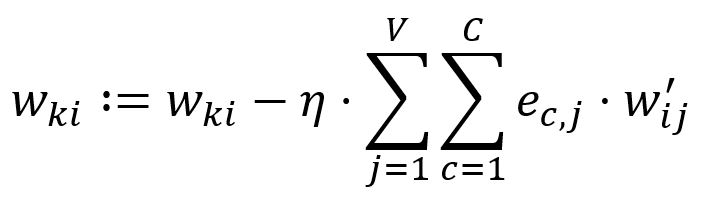
Dans notre exemple, , donc, et sont mis à jour:
Optimisation
Nous avons exploré les principes fondamentaux du modèle Skip-gram. Néanmoins, incorporer des optimisations est impératif pour garantir que la complexité computationnelle du modèle demeure viable et pragmatique pour les applications du monde réel. Cliquez ici pour continuer à lire.

