Qu'est-ce que l'Intégration de Graph ?
L'intégration de graph est une technique qui produit les représentations en vecteurs latents pour les graphs. L'intégration de graph peut être effectuée à différents niveaux du graph, les deux niveaux prédominants sont :
- Intégration de Node - Associe chaque node du graph à un vecteur.
- Intégration de Graph - Associe le graph entier à un vecteur.
Chaque vecteur issu de ce processus est également appelé intégration ou représentation.
Le terme "latent" suggère que ces vecteurs sont inférés ou appris à partir des données. Ils sont créés d'une manière qui préserve la structure (comment les nodes sont connectés) et/ou les attributs (propriétés des nodes et des edges) à l'intérieur du graph, qui pourraient ne pas être immédiatement apparents.
Prenant l'intégration de node comme exemple, les nodes qui sont plus similaires dans le graph auront des vecteurs qui sont plus proches les uns des autres dans l'espace de vecteurs.
Pour fournir une illustration, ci-dessous montrent les résultats (à droite) de l'exécution de l'algorithme d'intégration de node DeepWalk sur le graph du club de karaté de Zachary (à gauche). Dans le graph, les couleurs des nodes indiquent un regroupement basé sur la modularité. Une fois que tous les nodes ont été transformés en vecteurs bidimensionnels, il devient évident que les nodes au sein de la même communauté sont positionnés relativement plus proches les uns des autres.
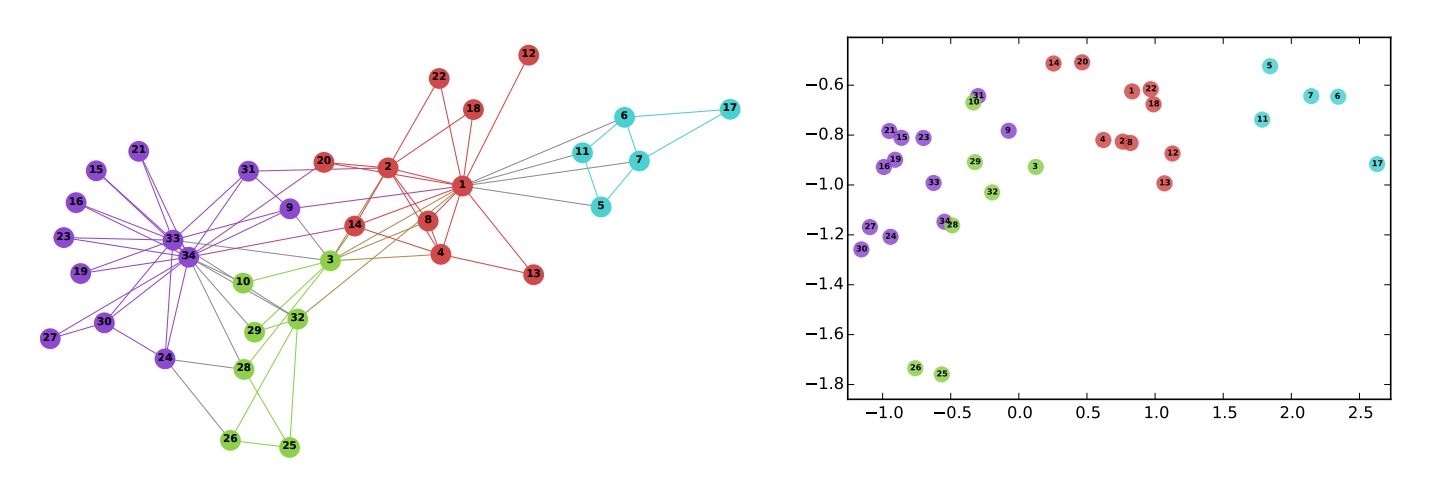 B. Perozzi, et al., DeepWalk: Online Learning of Social Representations (2014)
B. Perozzi, et al., DeepWalk: Online Learning of Social Representations (2014)Proximité des Intégrations
La notion de proximité parmi les intégrations se réfère généralement à la proximité des vecteurs représentant les nodes ou d'autres éléments du graph dans l'espace d'intégration. En essence, les intégrations qui affichent une proximité spatiale dans l'espace vectoriel indiquent un certain degré de similarité au sein du graph original.
En pratique, évaluer la proximité des intégrations implique d'employer diverses mesures de distance ou de similarité, telles que la Distance Euclidienne et Cosine Similarity.
Dimension d'Intégration
Le choix de la dimension d'intégration, également connue sous le nom de taille du vecteur, dépend de facteurs comme la complexité des données, les tâches spécifiques, et les ressources computationnelles. Bien qu'il n'y ait pas de réponse universelle, une fourchette typique de dimensions d'intégration en pratique se situe entre 50 et 300.
Des intégrations plus petites facilitent des calculs et comparaisons plus rapides. Une approche recommandée est de commencer avec une dimension plus petite et de l'élargir progressivement au besoin, en se basant sur l'expérimentation et la validation par rapport aux métriques de performance pertinentes à votre application.
Pourquoi l'Intégration de Graph ?
Réduction Dimensionalité
Les graphs sont souvent considérés comme de haute dimension en raison des relations complexes qu'ils encapsulent, plutôt que des dimensions physiques qu'ils occupent.
L'intégration de graph fonctionne comme une méthode de réduction de dimensionnalité qui s'efforce de capturer les informations les plus importantes des données du graph tout en réduisant substantiellement la complexité et les défis computationnels associés aux hautes dimensions. Dans le domaine de la réduction de dimensionnalité et de l'intégration, même quelques centaines de dimensions sont toujours étiquetées comme de basse dimension par rapport aux données originalement de haute dimension.
Compatibilité Améliorée en Science des Données
Les espaces vectoriels offrent des dizaines d'avantages par rapport aux graphs en termes d'intégration harmonieuse avec des approches mathématiques et statistiques dans le domaine de la science des données. À l'inverse, les graphs, constitués de nodes et d'edges, sont limités à n'employer que des sous-ensembles spécifiques de ces méthodologies.
L'avantage inhérent des vecteurs réside dans leur adaptation naturelle aux opérations mathématiques et techniques statistiques, car chaque vecteur incarne un ensemble de caractéristiques numériques. Des opérations de base comme l'addition et les produits scalaires se manifestent avec simplicité et efficacité computationnelle dans les espaces vectoriels. Cette efficacité se traduit fréquemment par des calculs plus rapides lorsqu'on les compare aux opérations analogues effectuées sur des graphs.
Comment l'Intégration de Graph est-elle Utilisée ?
L'intégration de graph sert de pont, agissant comme une étape de prétraitement pour les graphs. Une fois que nous générons des intégrations pour les nodes, edges, ou graphs, nous pouvons tirer parti de ces intégrations pour diverses tâches à venir. Ces tâches incluent la classification des nodes, la classification des graphs, la prédiction de liens, le regroupement et la détection de communautés, la visualisation, et plus encore.
Analyse Graphique
Nous disposons d'un ensemble d'algorithmes de graph répondant à divers objectifs d'analyse de graph. Bien qu'ils offrent un aperçu précieux, ils ont des limites. Souvent dépendants de fonctionnalités faites à la main extraites des matrices d'adjacence, ces algorithmes pourraient ne pas capturer entièrement les nuances de données complexes. En outre, exécuter efficacement ces algorithmes sur des graphs à grande échelle nécessite un effort computationnel significatif.
C'est là que l'intégration graphique entre en jeu. En créant des représentations en basse dimension, les intégrations fournissent des entrées plus riches et plus adaptables pour un large éventail d'analyses et de tâches. Ces vecteurs appris renforcent l'efficacité et la précision de l'analyse graphique, surpassant l'exécution directe dans le domaine des graphs de haute dimension.
Considérons le cas de l'analyse de similarité de node. Les algorithmes de similarité conventionnels se divisent généralement en deux catégories : la similarité basée sur le voisinage et la similarité basée sur les propriétés. La première, illustrée par la Jaccard Similarity et la Overlap Similarity, s'appuie sur le voisinage à 1 saut des nodes et calcule des scores de similarité. La seconde, représentée par la Distance Euclidienne et la Cosine Similarity, utilise plusieurs propriétés numériques des nodes pour calculer les scores de similarité basés sur les valeurs des propriétés.
Bien que ces méthodes aient leurs mérites, elles capturent souvent seulement les caractéristiques superficielles des nodes, limitant ainsi leur applicabilité. En revanche, encapsuler les nodes avec des informations latentes et avancées du graph enrichit les données d'entrée pour ces algorithmes de similarité. Cette fusion permet aux algorithmes de considérer des relations plus sophistiquées, conduisant à des analyses plus significatives.
Apprentissage Machine & Apprentissage Profond
Les techniques contemporaines d'apprentissage machine (ML) et d'apprentissage profond (DL) ont révolutionné divers domaines. Pourtant, les appliquer directement aux graphs présente des défis uniques. Les graphs possèdent des caractéristiques distinctes des données structurées traditionnelles (par exemple, des données tabulaires), les rendant moins adaptées aux méthodes ML/DL standard.
Bien qu'il existe des moyens d'appliquer ML/DL aux graphs, l'intégration graphique s'avère une méthode simple et efficace. En convertissant les graphs ou éléments de graph en vecteurs continus, les intégrations non seulement abstraient les complexités de tailles de graph arbitraires et de topologies dynamiques, mais s'harmonisent également bien avec les ensembles d'outils et bibliothèques ML/DL modernes.
Cependant, transformer les données dans un format digeste pour ML/DL n'est pas suffisant. L'apprentissage des caractéristiques est également un défi significatif avant d'entrer des données dans les modèles ML/DL. L'ingénierie traditionnelle des caractéristiques est à la fois chronophage et moins précise. Les intégrations, servant de caractéristiques apprises qui encapsulent à la fois des informations structurelles et attributives, amplifient la compréhension du modèle des données.
Imaginez un réseau social où les nodes représentent des individus et les edges décrivent des connexions sociales. La tâche est de prédire l'affiliation politique des individus. Une approche traditionnelle pourrait impliquer l'extraction de caractéristiques faites à la main telles que le nombre d'amis, l'âge moyen des amis, et le niveau d'éducation des voisins pour chaque individu. Ces caractéristiques seraient ensuite introduites dans un modèle ML comme un arbre de décision ou une forêt aléatoire. Cependant, cette approche échoue à capturer toutes les nuances des données, traitant les connexions sociales de chaque individu comme des caractéristiques séparées et négligeant les relations complexes au sein du graph.
En revanche, l'utilisation des intégrations graphiques permet la création d'intégrations plus sophistiquées pour chaque individu, produisant des prédictions précises et contextuellement informées.

