Vue d’ensemble
Un tri topologique d'un graphe dirigé est un ordonnancement de ses nodes en une séquence, où le node de départ de chaque edge apparaît avant son node d'arrivée. Le tri topologique n'est applicable qu'aux graphes dirigés acycliques (DAGs) qui ne contiennent aucun cycle.
Le tri topologique a diverses applications en informatique et dans d'autres domaines. Dans la gestion de projet et la planification de tâches, le tri topologique joue un rôle crucial pour déterminer l'ordre optimal d'exécution des tasks en fonction de leurs dépendances. Il est également utile pour résoudre les dépendances entre modules, bibliothèques ou composants dans le développement de logiciels. En utilisant cet algorithme, les dépendances peuvent être résolues dans la séquence correcte, atténuant les conflits et les erreurs potentielles.
Concepts
Graphe Dirigé Acyclique (DAG)
Un graphe dirigé acyclique (DAG) est un type de graphe dirigé sans cycles dirigés. Autrement dit, il n'est pas possible de commencer à n'importe quel node v et de suivre un path dirigé pour revenir à v dans un DAG.
Comme montré ici, les premier et second graphes sont des DAGs, tandis que le troisième graphe contient un cycle dirigé (B→C→D→B) et ne qualifie donc pas en tant que DAG.
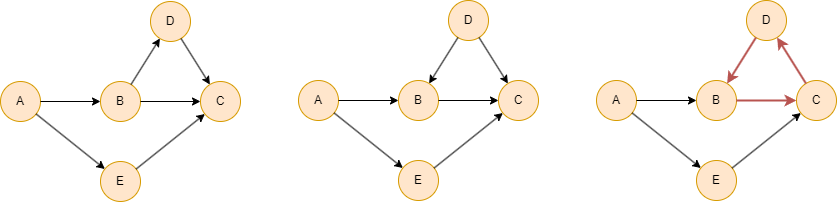
Un graphe dirigé est un DAG si et seulement s'il peut être trié topologiquement.
Tri Topologique
Chaque DAG a au moins un tri topologique.
Dans les exemples ci-dessus, les nodes du premier graphe ont 3 tris possibles :
- A, E, B, D, C
- A, B, E, D, C
- A, B, D, E, C
Un DAG a un tri topologique unique si et seulement s'il possède un path dirigé contenant tous les nodes, auquel cas le tri est le même que l'ordre dans lequel les nodes apparaissent dans le path.
Dans l'exemple suivant, les nodes n'ont qu'un seul tri possible : A, B, D, C, E, F.
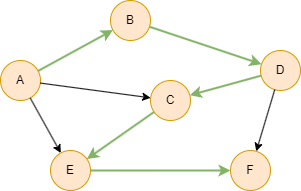
Considérations
Exécuter l'algorithme de tri topologique sur un graphe avec des cycles entraînera l'omission de certains nodes. Les nodes omis sont :
- Les nodes qui font partie d'un cycle (y compris les auto-cycles).
- Les nodes qui sont accessibles à partir des nodes ci-dessus par des edges sortants.
Dans l'exemple donné, il faut d'abord omettre les nodes C, D et G, qui forment le cycle. Ensuite, les nodes F, J et H qui sont accessibles depuis ces derniers sont également omis. En conséquence, le résultat du tri topologique est A, I, B, E.
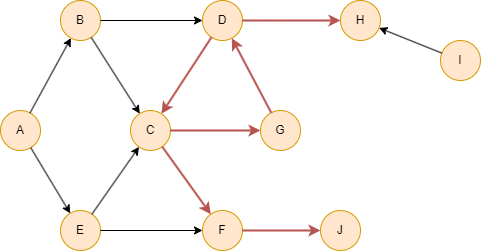
Si un graphe est déconnecté, ou devient déconnecté après avoir omis les nodes qui forment le cycle et les nodes influencés par eux, le tri topologique est effectué au sein de chaque composant connecté. Les résultats de tri sont ensuite renvoyés de manière cohérente dans tous les composants. Les nodes isolés sont également inclus dans les résultats et ne sont pas négligés.
Syntaxe
- Commande :
algo(topological_sort) - Cet algorithme n'a pas de paramètres.
Exemples
Le graphe d'exemple est le suivant :
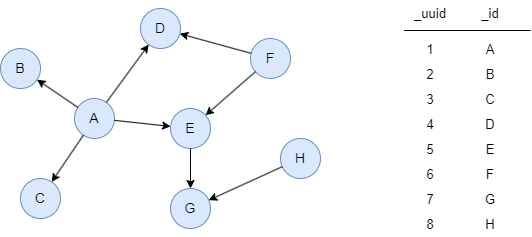
File Writeback
| Spec | Contenu |
|---|---|
| filename | _id,_id,... |
algo(topological_sort).params().write({
file: {
filename: 'sort'
}
})
Résultats : Fichier sort
H
F
A
B
C
D
E
G
Direct Return
Alias Ordinal |
Type |
Description |
|---|---|---|
| 0 | []nodes |
Tableau de nodes triés |
algo(topological_sort).params() as nodes
return nodes
Résultats : nodes
| 8 |
| 6 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 7 |
Stream Return
Alias Ordinal |
Type |
Description |
|---|---|---|
| 0 | []nodes |
Tableau de nodes triés |
algo(topological_sort).params().stream() as n
find().nodes(n) as nodes
return nodes{*}
Résultats : nodes
| _id | _uuid |
|---|---|
| H | 8 |
| F | 6 |
| A | 1 |
| B | 2 |
| C | 3 |
| D | 4 |
| E | 5 |
| G | 7 |

