Vue d’ensemble
Fast Random Projection (ou FastRP) est un algorithme évolutif et performant pour l'apprentissage des représentations de node dans un graph. Il réalise un calcul itératif des embeddings de node avec deux composants : premièrement, la construction de la matrice de similarité de node ; deuxièmement, la réduction dimensionnelle par projection aléatoire.
FastRP a été proposé par H. Chen et al. en 2019 :
- H. Chen, S.F. Sultan, Y. Tian, M. Chen, S. Skiena, Fast and Accurate Network Embeddings via Very Sparse Random Projection (2019)
Cadre FastRP
Les auteurs de FastRP proposent que la plupart des méthodes d'embedding de réseau consistent essentiellement en deux composants : (1) construire une matrice de similarité de node ou échantillonner implicitement des paires de nodes à partir de celle-ci, puis (2) appliquer des techniques de réduction dimensionnelle à cette matrice.
En ce qui concerne la réduction dimensionnelle, de nombreux algorithmes populaires, comme Node2Vec, reposent sur des méthodes chronophages telles que Skip-gram. Les auteurs soutiennent que le succès de ces méthodes devrait être attribué à la construction correcte de cette matrice de similarité, plutôt qu'à la méthode de réduction dimensionnelle employée.
Par conséquent, FastRP utilise la projection aléatoire très rare, qui est une méthode évolutive sans optimisation pour la réduction dimensionnelle.
Projection Aléatoire Très Rare
La projection aléatoire est une méthode de réduction dimensionnelle qui préserve approximativement les distances relatives par paire entre les points de données lorsqu'ils sont intégrés de l'espace de haute dimension vers un espace de basse dimension. Les garanties théoriques de la projection aléatoire sont principalement dérivées du Lemme de Johnson-Lindenstrauss.
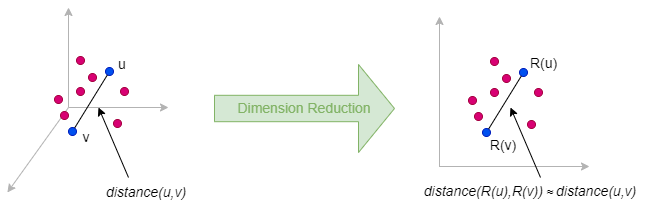
L'idée derrière la projection aléatoire est très simple : pour réduire une matrice Mn×m (pour les données de graph, nous avons n = m) à une matrice Nn×d où d ≪ n, nous pouvons simplement multiplier M par une matrice de projection aléatoire Rm×d : N = M ⋅ R.
La matrice R est générée en échantillonnant ses entrées indépendamment à partir d'une distribution aléatoire. Plus précisément, FastRP envisage la méthode de projection aléatoire très rare pour la réduction dimensionnelle, où les entrées de R sont échantillonnées à partir de la distribution suivante :

et s=sqrt(m).
La projection aléatoire très rare a une efficacité de calcul supérieure puisqu'elle ne nécessite que la multiplication matricielle, et (1-1/s) des entrées de R sont nulles.
De plus, Ultipa prend en charge l'initialisation de la matrice R avec une combinaison de certaines propriétés numériques sélectionnées de node (features). Dans ce cas, chaque ligne de la matrice R est formée par la concaténation de deux parties :

- Les éléments d1 ~ dx sont générés par l'algorithme de Projection Aléatoire Très Rare.
- Les éléments p1 ~ py sont une combinaison linéaire des valeurs des propriétés de node sélectionnées.
- x + y est égal à la dimension des embeddings finaux, où y est appelé la dimension de la propriété.
- Le nombre de features de node sélectionnés n'a pas besoin d'être égal à la dimension des propriétés.
Construction de la Matrice de Similarité de Node
FastRP garde deux caractéristiques clés lors de la construction de la matrice de similarité de node :
- Préserver la proximité d'ordre élevé dans le graph
- Effectuer une normalisation élément par élément sur la matrice
Soit S la matrice d'adjacence du graph G =(V,E), D la matrice de degré, et A la matrice de transition et A = D-1S. Voir l'exemple ci-dessous, le nombre sur chaque edge représente le poids de l'edge :

Le fait est que dans la matrice A, l'entrée Aij représente la probabilité que le node i atteigne le node j avec une marche aléatoire de 1 étape. De plus, si on élève A à la puissance k pour obtenir la matrice Ak, alors Akij dénote la probabilité d'atteindre le node j à partir du node i en k étapes de marche aléatoire. Ainsi, la matrice Ak préserve la proximité d'ordre élevé du graph.
Cependant, lorsque k → ∞, il peut être prouvé que Akij → dj/2m où m = |E|, et dj est le degré du j-ième node. Étant donné que de nombreux graph du monde réel sont sans échelle, les entrées dans Ak suivent une distribution à queue lourde. Cela implique que les distances par paire entre les points de données dans Ak sont principalement influencées par des colonnes avec des valeurs exceptionnellement grandes, les rendant moins significatives et posant des défis pour la prochaine étape de réduction dimensionnelle.
Pour remédier à cela, FastRP effectue en outre une normalisation sur la matrice Ak en la multipliant par une matrice de normalisation diagonale L, où Lij = (dj/2m)β, et β est la force de normalisation. La force de normalisation contrôle l'impact du degré de node sur les embeddings : lorsque β est négatif, l'importance des voisins de haut degré est diminuée, et l'inverse lorsque β est positif.
Processus de l'Algorithme
L'algorithme FastRP suit ces étapes :
- Générer la matrice de projection aléatoire R.
- Réduire la dimension de la matrice de transition normalisée à 1 étape : N1 = A ⋅ L ⋅ R
- Réduire la dimension de la matrice de transition normalisée à 2 étapes : N2 = A ⋅ (A ⋅ L ⋅ R) = A ⋅ N1
- Répéter l'étape 3 jusqu'à la matrice de transition normalisée à k étapes : Nk = A ⋅ Nk-1
- Générer la combinaison pondérée de différentes puissances de A : N = α1N1 + ... + αkNk, où α1,...,αk sont les poids d'itération.
L'efficacité de FastRP bénéficie également de la propriété associative de la multiplication matricielle. Il ne calcule pas Ak à partir de zéro, car le calcul peut être effectué de manière itérative.
Considérations
- L'algorithme FastRP ignore la direction des edges mais les calcule comme des edges non-dirigés.
Syntaxe
- Commande :
algo(fastRP) - Paramètres :
Nom |
Type |
Spec |
Défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| dimension | int | ≥2 | / | Non | Dimensionnalité des embeddings |
| normalizationStrength | float | / | / | Oui | Force de normalisation β |
| iterationWeights | []float | >0 | [0.0,1.0,1.0] | Oui | Poids pour chaque itération, la taille du tableau est le nombre d'itérations |
| edge_schema_property | []@<schema>?.<property> |
Type numérique, doit être LTE | / | Oui | Propriété(s) d'edge utilisée(s) comme poids de edge(s), où les valeurs de plusieurs propriétés sont additionnées |
| node_schema_property | []@<schema>?.<property> |
Type numérique, doit être LTE | / | Oui | Propriété(s) de node utilisée(s) comme feature(s) ; propertyDimension and node_schema_property doivent être configurés ensemble ou être tous deux ignorés |
| propertyDimension | int | (0,dimension] |
/ | Oui | Longueur de la dimension de la propriété ; propertyDimension and node_schema_property doivent être configurés ensemble ou être tous deux ignorés |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
Exemple
File Writeback
| Spec | Contenu |
|---|---|
| filename | _id, embedding_result |
algo(fastRP).params({
dimension : 10,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 1],
edge_schema_property: ['w1', 'w2'],
node_schema_property: ['@default.f1', '@default.f2'],
propertyDimension: 3
}).write({
file:{
filename: 'embedding'
}
})
Property Writeback
| Spec | Contenu | Écrire dans | Type de Donnée |
|---|---|---|---|
| property | embedding_result |
Node Property | string |
algo(fastRP).params({
dimension : 10,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 1],
edge_schema_property: ['w1', 'w2']
}).write({
db:{
property: 'embedding'
}
})
Direct Return
| Alias Ordinal | Type |
Description |
Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et ses embeddings | _uuid, embedding_result |
algo(fastRP).params({
dimension : 10,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 1]
}) as embeddings
return embeddings
Stream Return
| Alias Ordinal | Type |
Description |
Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et ses embeddings | _uuid, embedding_result |
algo(fastRP).params({
dimension : 10,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 1]
}).stream() as embeddings
return embeddings

