Vue d’ensemble
Un parcours aléatoire commence à un certain node dans un graph et progresse en se déplaçant aléatoirement vers un de ses nodes voisins ; ce process est souvent répété pour un nombre défini d'étapes. Ce concept a été introduit par le mathématicien et biostatisticien britannique Karl Pearson en 1905, et il est depuis devenu une pierre angulaire de l'étude de divers systèmes, aussi bien dans qu'au-delà de la théorie des graph.
- K. Pearson, The Problem of the Random Walk (1905)
Concepts
Marche Aléatoire
La marche aléatoire est une modèle mathématique utilisé pour simuler une série de pas faits de manière stochastique ou imprévisible, telle la trajectoire erratique d'une personne ivre.
La marche aléatoire de base est effectuée dans un espace unidimensionnel : un node initie à partir de l'origine d'une ligne numérique et se déplace vers le haut ou vers le bas d'une unité à la fois avec une probabilité égale. Un exemple d'une marche aléatoire de 10 étapes est le suivant:
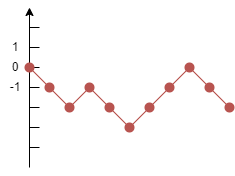
Voici un exemple de la réalisation de cette marche aléatoire plusieurs fois, chaque marche consistant en 100 étapes:
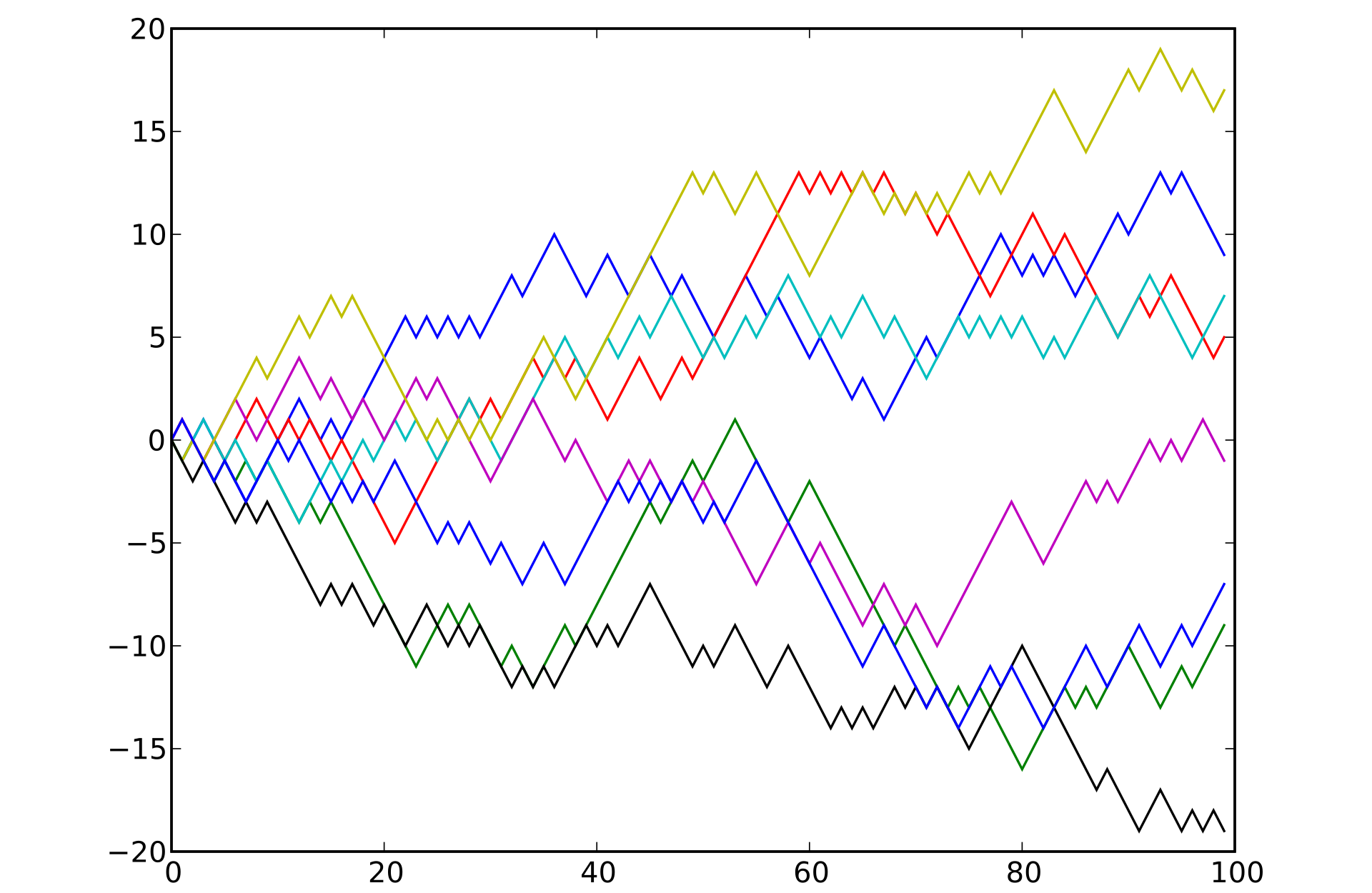
Marche Aléatoire dans un Graph
Dans un graph, une marche aléatoire est un processus où un chemin est formé en commençant par un nœud et en se déplaçant séquentiellement à travers les nœuds voisins. Ce processus est contrôlé par la profondeur de marche, qui détermine le nombre de nodes à visiter.
L'algorithme Random Walk d'Ultipa implémente la forme classique de parcours aléatoire. Par défaut, chaque edge est assignée à un poids égal (égal à 1), entraînant des probabilités égales de traversée. Lorsque des poids d'edge sont spécifiés, la probabilité de traverser ces edges devient proportionnelle à leurs poids. Il est important de noter qu'il existe diverses variations du parcours aléatoire, comme le Node2Vec Walk et le Struc2Vec Walk.
Considérations
- Les boucles auto-traversées sont également éligibles pour être traversées pendant la marche aléatoire.
- Si la marche commence à partir d'un node isolé sans aucune boucle auto-traversée, la marche s'arrête après la première étape car il n'y a pas d'edges adjacents vers lesquels procéder.
- L'algorithme Random Walk ignore la direction des edges mais les calcule comme des edges non orientées.
Syntaxe
- Commande:
algo(random_walk) - Paramètres:
| Nom | Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
| ids / uuids | []_id / []_uuid |
/ | / | Oui | ID/UUID des nodes pour commencer les parcours aléatoires ; démarre à partir de tous les nodes si non défini |
| walk_length | int | ≧1 | 1 |
Oui | Profondeur de chaque parcours, c’est-à-dire, le nombre de nodes à visiter |
| walk_num | int | ≧1 | 1 |
Oui | Nombre de parcours à effectuer pour chaque node spécifié |
| edge_schema_property | []@<schema>?.<property> |
Type numérique, doit être LTE | / | Oui | Propriété(s) d'edge à utiliser comme poids d’edge, où les valeurs de plusieurs propriétés sont additionnées ; les nodes ne marchent qu'along des edges avec la propriété spécifiée |
| limit | int | ≧-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
Exemple
Le graph exemple est le suivant, les nombres sur les edges sont les valeurs de la propriété d'edge score:
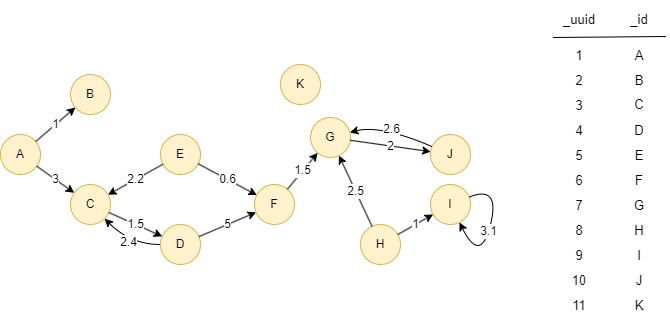
File Writeback
Spec |
Content |
Description |
|---|---|---|
| filename | _id,_id,... |
IDs des nodes visités |
algo(random_walk).params({
walk_length: 6,
walk_num: 2
}).write({
file:{
filename: 'walks'
}})
Résultats: Fichier walks
K,
J,G,J,G,F,D,
I,I,I,H,I,I,
H,I,I,I,I,I,
G,J,G,J,G,H,
F,D,C,A,B,A,
E,F,D,C,D,C,
D,F,G,H,G,H,
C,D,F,E,F,D,
B,A,B,A,C,A,
A,C,A,C,D,F,
K,
J,G,J,G,J,G,
I,I,I,H,I,I,
H,I,H,G,J,G,
G,H,I,I,H,G,
F,D,C,D,F,E,
E,C,D,F,G,J,
D,C,D,C,E,F,
C,E,C,A,B,A,
B,A,B,A,C,A,
A,B,A,C,D,C,
Direct Return
| Alias Ordinal | Type | Description |
Columns |
|---|---|---|---|
| 0 | []perWalk | Tableau des UUID des nodes visités | [_uuid, _uuid, ...] |
algo(random_walk).params({
walk_length: 6,
walk_num: 2,
edge_schema_property: 'score'
}) as walks
return walks
Résultats: walks
| [11] |
| [10, 7, 10, 7, 10] |
| [9, 9, 9, 9, 9] |
| [8, 9, 9, 9, 9] |
| [7, 10, 7, 10, 7] |
| [6, 4, 3, 4, 3] |
| [5, 6, 7, 6, 4] |
| [4, 6, 7, 10, 7] |
| [3, 1, 3, 1, 3] |
| [2, 1, 3, 1, 3] |
| [1, 3, 4, 3, 5] |
| [11] |
| [10, 7, 10, 7, 10] |
| [9, 9, 9, 8, 7] |
| [8, 9, 8, 7, 8] |
| [7, 6, 4, 6, 4] |
| [6, 5, 6, 4, 6] |
| [5, 3, 4, 6, 4] |
| [4, 6, 4, 6, 7] |
| [3, 4, 3, 4, 6] |
| [2, 1, 3, 1, 3] |
| [1, 2, 1, 3, 1] |
Stream Return
| Alias Ordinal | Type | Description |
Columns |
|---|---|---|---|
| 0 | []perWalk | Tableau des UUID des nodes visités | [_uuid, _uuid, ...] |
algo(random_walk).params({
walk_length: 5,
walk_num: 1,
edge_schema_property: '@default.score'
}).stream() as walks
where size(walks) == 5
return walks
Résultats: walks
| [10, 7, 10, 7, 6] |
| [9, 9, 9, 9, 9] |
| [8, 9, 9, 9, 9] |
| [7, 10, 7, 6, 4] |
| [6, 4, 3, 4, 6] |
| [5, 6, 4, 6, 4] |
| [4, 3, 4, 6, 4] |
| [3, 1, 3, 5, 3] |
| [2, 1, 3, 4, 6] |
| [1, 2, 1, 2, 1] |

