In the realm of graph computing, the query for neighbors of a node is also known as the K-hop query, with "K" defining the shortest distance between these neighbors and the focal node. K-Hop queries find interesting applications across industries and research fields. Impact or risk analysis, for instance, tracks the spread of a disease by identifying individuals within a certain proximity of an infected person.
A Real Test
K-hop queries yield definitive results. First of all, regardless of how many possible routes exist between nodes, K-hop query cares solely the shortest path(s). When ignoring edge weights, the number of edges in the shortest path defines the K. As the example shows, D is the 2-hop neighbor of A, but not a 3-hop neighbor.
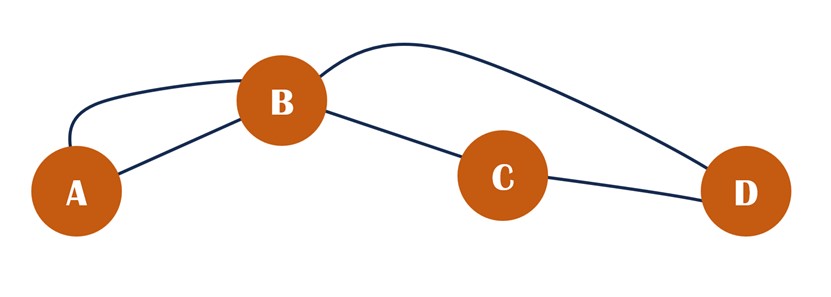
Secondly, K-hop neighbors should be de-duplicated. In cases where multiple shortest paths are found, each neighbor is still counted only once. Consequently, the 1-hop neighborhood of A is {B} rather than {B, B}.
These two points uphold the accuracy of K-hop queries. As the graph size expands to encompass millions or even billions of nodes and edges, and the required query depth increases to 6, 15 or even exceeds 20, the computational pressure loaded on the graph computing engine intensifies significantly. Manual verification of results becomes impractical, with many graph databases or graph-computing frameworks unable to guarantee returns in such scenarios, or correctness of results.
The ability to execute a 6-hop query for a node in a large graph (like Twitter-2010 dataset) within 10 seconds is indicative of a Real-time Graph System. Traversing 6 hops from most nodes in the Twitter dataset would touch over 99% of its all 1.5 billion edges and nodes, equating to traversing over 150 million nodes and edges per second.
For the K-hop query, Ultipa offers slews of optimization for the traversal and deduplication mechanisms, ensuring both accuracy and efficiency. Therefore, we recommend you use the K-hop queries whenever they can achieve the same outcome as other query types.
Example: Counting Distinct Values
Consider the following UQL query executed on a Display_Ad_Click dataset, containing over 1 million users and 0.8 million online ads. The dataset captures user behaviors of clicking ads over some days, represented by edges, resulting in approximately 1.3 million clicks recorded.
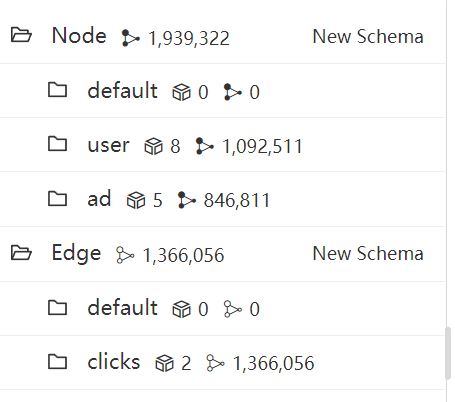
Number of nodes and edges in the dataset
find().nodes({@user.shopping_level == 1}) as u
call {
with u
n(u).e({@clicks}).n({@ad} as ads)
with count(DISTINCT ads) as adsCount
return adsCount
}
order by adsCount desc limit 5
return table(u._id, adsCount)The objective of this query is to determine the distinct ads clicked by each user at the 1st shopping level and rank the top 5 users based on the count of distinct ads.
| u._id | adsCount |
| u853650 | 103 |
| u341347 | 84 |
|
u642926
|
70 |
| u74383 | 65 |
| u950625 | 64 |
Results of the query
This query employs an n().e().n() path template to search for the ads clicked by individual users. The use of the operator DISTINCT is necessary when counting the ads due to the possibility of users clicking on the same ad repeatedly.
Ad-clicking records of an user
Let’s examine the query plan and time cost by adding the PROFILE prefix to the UQL statement. In my testing environment, the query took a total of 35,450ms (millisecond) to generate the final table, with a substantial 33,002ms spent on the path template queries.

Use the K-Hop Query
The requirement for distinct values makes us to consider using the performant K-hop query instead. Since the results of K-hop query is already de-duplicated, the DISTINCT used in the count() function is also saved.
find().nodes({@user.shopping_level == 1}) as u
call {
with u
khop().n(u).e({@clicks}).n({@ad}) as ads
with count(ads) as adsCount
return adsCount
}
order by adsCount desc limit 5
return table(u._id, adsCount)This UQL yielded identical results but in just 2,030ms, with the K-hop path template query completing in only 771ms – a notable speed improvement of over 42 times. With 74,612 users at the 1st shopping level involved, the K-hop query for each one took only about 0.01ms.
 Final Remarks
Final Remarks
The exemplary performance of Ultipa’s K-hop query is remarkable and competitive. Proper utilization of the K-hop query can achieve substantial speed improvement in the data analytics processes. When evaluating graph systems, it’s imperative to consider the effectiveness of the K-hop query.

