Overview
The K-1 Coloring algorithm assigns colors to each node such that no two adjacent nodes share the same color, and the number of colors used is minimized.
- U.V. Çatalyürek, J. Feo, A.H. Gebremedhin, M. Halappanavar, A. Pothen, Graph Coloring Algorithms for Multi-core and Massively Multithreaded Architectures (2018)
Concepts
Distance-1 Graph Coloring
Distance-1 graph coloring, also known as K-1 graph coloring, is a concept in graph theory where the goal is to assign colors (represented by integers 0, 1, 2, ...) to the nodes of a graph such that no two nodes that are at distance 1 from each other (i.e., adjacent nodes) should have the same color. The objective of the problem is also to minimize the number of colors used.
One of the most famous applications of graph coloring is geographical map coloring, which is to color the regions of a map (represented as nodes) such that no two adjacent regions (which share a border) have the same color.
The concept also has many other practical applications. For example, in schools, you may need to schedule classes without conflicts. Each class is represented as a node, and edges represent conflicts (e.g., if two classes require the same room). By coloring the graph, each class is assigned a "color", which corresponds to a different time slot.
Greedy Coloring Algorithm
The graph coloring problem is known to be NP-hard when solved optimally. Solutions that are near-optimal can be obtained using a greedy algorithm.
Serial Greedy Coloring Algorithm
At the start of the greedy algorithm, each node v in the graph has its color initialized to uncolored. The algorithm processes each node v as below:
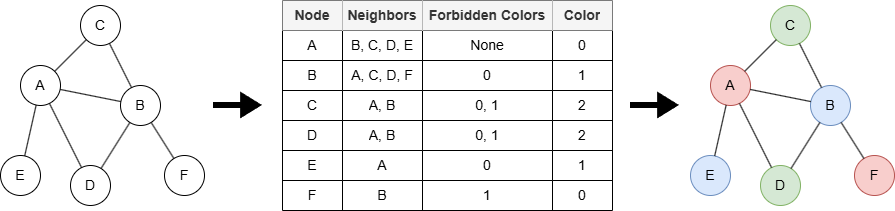
- For every adjacent node
wofv, mark the color ofwas forbidden forv. - Assign the smallest available color to
vthat is different from all its forbidden colors.
The algorithm assigns colors to nodes sequentially, which can become a bottleneck for large graphs. The algorithm below instead allows multiple nodes to be processed in parallel, with careful handling of potential conflicts.
Iterative Parallel Greedy Coloring Algorithm
The iterative parallel greedy coloring algorithm is a parallelized extension of the serial greedy coloring algorithm. It is designed to take advantage of modern multicore and distributed computing systems to handle large graphs more efficiently.
The algorithm divides nodes in the graph into independent sets to proceed in multiple parallel threads. Each iteration has two phases:
- Tentative coloring phase: It is the same as the serial greedy coloring algorithm, except that it is concurrently run by multiple threads.
- Conflict detection phase: Each thread identifies a subset of nodes that needs to be re-colored in the next iteration to resolve any conflicts, i.e., two adjacent nodes (in different threads) get the same color.
The algorithm terminates when no more nodes to be re-colored are left.
Considerations
- The K-1 Coloring algorithm ignores the direction of edges.
Example Graph
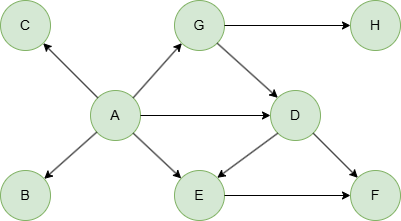
To create this graph:
// Runs each row separately in order in an empty graphset
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"}])
insert().into(@default).edges([{_from:"A", _to:"B"}, {_from:"A", _to:"C"}, {_from:"A", _to:"D"}, {_from:"A", _to:"E"}, {_from:"A", _to:"G"}, {_from:"D", _to:"E"}, {_from:"D", _to:"F"}, {_from:"E", _to:"F"}, {_from:"G", _to:"D"}, {_from:"G", _to:"H"}])
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as hdc_coloring:
CALL hdc.graph.create("hdc-server-1", "hdc_coloring", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static",
query: "query",
default: false
})
hdc.graph.create("hdc_coloring", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static",
query: "query",
default: false
}).to("hdc-server-1")
Parameters
Algorithm name: k1_coloring
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
loop_num |
Integer | ≥1 | 5 |
Yes | Number of iterations. The algorithm will terminate after completing all rounds. This option is only valid when version is set to 2. |
version |
Integer | 1, 2 |
2 |
Yes | Sets to 1 to run the serial greedy coloring algorithm, or 2 to run the iterative parallel greedy coloring algorithm. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results. |
In the results of this algorithm, nodes with the same color are considered to belong to the same community.
File Writeback
This algorithm can generate three files:
Spec |
Content |
|---|---|
filename_community_id |
|
filename_ids |
|
filename_num |
|
CALL algo.k1_coloring.write("hdc_coloring", {
params: {
return_id_uuid: "id",
version: 1
},
return_params: {
file: {
filename_community_id: "f1.txt",
filename_ids: "f2.txt",
filename_num: "f3.txt"
}
}
})
algo(k1_coloring).params({
projection: "hdc_coloring",
return_id_uuid: "id",
version: 1
}).write({
file: {
filename_community_id: "f1.txt",
filename_ids: "f2.txt",
filename_num: "f3.txt"
}
})
Result:
_id,community_id
D,1
F,2
H,1
B,1
A,2
E,0
C,0
G,0
community_id,_ids
0,E;C;G;
2,F;A;
1,D;H;B;
community_id,count
0,3
2,2
1,3
DB Writeback
Writes the community_id values from the results to the specified node property. The property type is uint32.
CALL algo.k1_coloring.write("hdc_coloring", {
params: {
loop_num: 10,
version: 2
},
return_params: {
db: {
property: "color"
}
}
})
algo(k1_coloring).params({
projection: "hdc_coloring",
loop_num: 10,
version: 2
}).write({
db: {
property: "color"
}
})
Stats Writeback
CALL algo.k1_coloring.write("hdc_coloring", {
params: {
version: 1
},
return_params: {
stats: {}
}
})
algo(k1_coloring).params({
projection: "hdc_coloring",
version:1
}).write({
stats: {}
})
Result:
| community_count |
|---|
| 3 |
Full Return
CALL algo.k1_coloring("hdc_coloring", {
params: {
return_id_uuid: "id",
loop_num: 5,
version: 2
},
return_params: {}
}) YIELD r
RETURN r
exec{
algo(k1_coloring).params({
return_id_uuid: "id",
loop_num: 5,
version: 2
}) as r
return r
} on hdc_coloring
Result:
| _id | community_id |
|---|---|
| D | 1 |
| F | 2 |
| H | 1 |
| B | 1 |
| A | 2 |
| E | 0 |
| C | 0 |
| G | 0 |
Stream Return
CALL algo.k1_coloring("hdc_coloring", {
params: {
return_id_uuid: "id",
loop_num: 15,
version: 1
},
return_params: {
stream: {}
}
}) YIELD r
RETURN r.community_id AS communityID, count(r) AS nodeCounts GROUP BY communityID
exec{
algo(k1_coloring).params({
return_id_uuid: "id",
loop_num: 15,
version: 1
}).stream() as r
group by r.community_id as communityID
with r, count(r) as nodeCounts
return table(communityID, nodeCounts)
} on hdc_coloring
Result:
| communityID | nodeCounts |
|---|---|
| 0 | 3 |
| 1 | 3 |
| 2 | 2 |
Stats Return
CALL algo.k1_coloring("hdc_coloring", {
params: {},
return_params: {
stats: {}
}
}) YIELD res
RETURN res
exec{
algo(k1_coloring).params().stats() as res
return res
} on hdc_coloring
Result:
| community_count |
|---|
| 3 |

